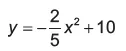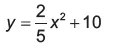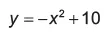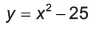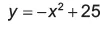Definição e Gráfico

01. (Enem 2024) Uma criança, utilizando um aplicativo, escreveu uma mensagem para enviar a um amigo. Essa mensagem foi escrita seguindo estas etapas:

Etapas Visor de escrita

A criança seguiu copiando e colando, em cada etapa, o que tinha no visor na etapa imediatamente anterior, até concluir a 20ª etapa. Em seguida, enviou a mensagem.

Qual foi o total de figuras contidas na mensagem enviada?

1. 3 x 2¹⁹
2. 3 x 2²⁰
3. 3 x 2²¹
4. 3 x 2²⁰ - 1
5. 3 x 2²⁰ - 3

02. (ENEM 2022) A trajetória de uma pessoa que pula de um andaime até o chão é descrita por uma função y = f (x), sendo x e y medidos em metro, conforme mostra a figura.

Seja D o domínio da função f (x), como definida na figura.

Para que a situação representada na figura seja real, o domínio dessa função deve ser igual a

1. {X2}, sendo x2 a raiz positiva de f (x).
2. {X ∈ ℝ | 0 ≤ X ≤ X2}, sendo x2 a raiz positiva de f (x).
3. {X ∈ ℝ | X1 ≤ X ≤ X2}, sendo x1 e x2 raízes de f (x), com x1 < x2.
4. {X ∈ ℝ | X ≥ 0}
5. X ∈ ℝ.

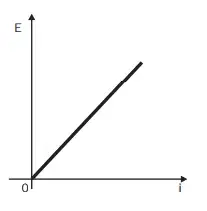
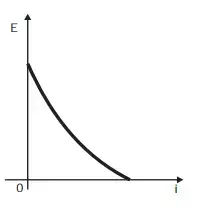
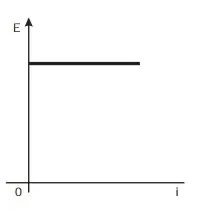
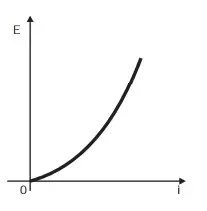
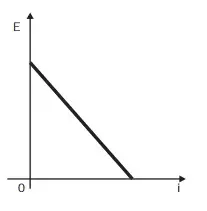
03. (Enem 2012) Existem no mercado chuveiros elétricos de diferentes potências, que representam consumos e custos diversos. A potência (P) de um chuveiro elétrico é dada pelo produto entre sua resistência elétrica (R) e o quadrado da corrente elétrica (i) que por ele circula. O consumo de energia elétrica (E), por sua vez, é diretamente proporcional à potência do aparelho.

Considerando as características apresentadas, qual dos gráficos a seguir representa a relação entre a energia consumida (E) por um chuveiro elétrico e a corrente elétrica (i) que circula por ele?

04. (Enem 2022) Uma máquina em operação tem sua temperatura T monitorada por meio de um registro gráfico, ao longo do tempo t. Essa máquina possui um pistão cuja velocidade V varia com a temperatura T da máquina, de acordo com a expressão V = T² - 4. Após a máquina funcionar durante o intervalo de tempo de 10 horas, o seu operador analisa o registro gráfico, apresentado na figura, para avaliar a necessidade de eventuais ajustes, sabendo que a máquina apresenta falhas de funcionamento quando a velocidade do pistão se anula.

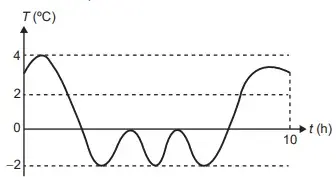
Quantas vezes a velocidade do pistão se anulou durante as 10 horas de funcionamento?

1. 1
2. 2
3. 3
4. 4
5. 5

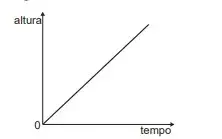
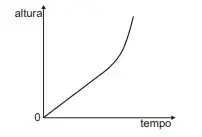
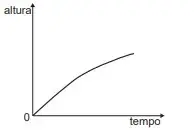
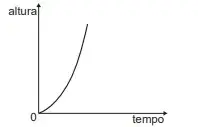
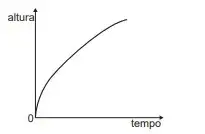
05. (Enem 2020) O consumo de espumantes no Brasil tem aumentado nos últimos anos. Uma das etapas do seu processo de produção consiste no envasamento da bebida em garrafas semelhantes às da imagem. Nesse processo, a vazão do líquido no interior da garrafa é constante e cessa quando atinge o nível de envasamento.

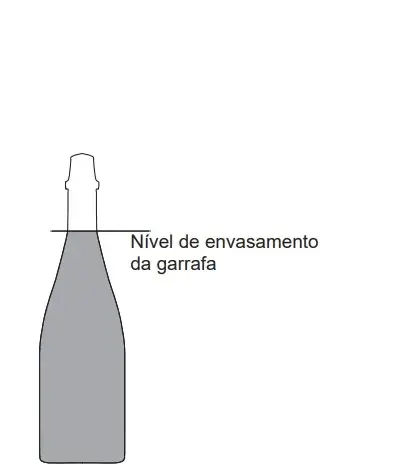
Qual esboço de gráfico melhor representa a variação da altura do líquido em função do tempo, na garrafa indicada na imagem?

06. (Enem 2014) A figura mostra uma criança brincando em um balanço no parque. A corda que prende o assento do balanço ao topo do suporte mede 2 metros. A criança toma cuidado para não sofrer um acidente, então se balança de modo que a corda não chegue a alcançar a posição horizontal. Na figura, considere o plano cartesiano que contém a trajetória do assento do balanço, no qual a origem está localizada no topo do suporte do balanço, o eixo X é paralelo ao chão do parque, e o eixo Y tem orientação positiva para cima.

A curva determinada pela trajetória do assento do balanço é parte do gráfico da função.

07. (Enem 2013) A parte interior de uma taça foi gerada pela rotação de uma parábola em torno de um eixo z, conforme mostra a figura.

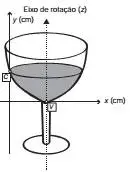
A função real que expressa a parábola, no plano cartesiano da figura, é dada pela lei f(x) = 3/2 x² - 6x + C, onde C é a medida da altura do líquido contido na taça, em centímetros. Sabe-se que o ponto V, na figura, representa o vértice da parábola, localizado sobre o eixo x.

Nessas condições, a altura do líquido contido na taça, em centímetros, é

1. 1.
2. 2.
3. 4.
4. 5.
5. 6.

08. (Enem PPL 2022) A trajetória de uma pessoa que pula de um andaime até o chão é descrita por uma função y = f (x), sendo x e y medidos em metro, conforme mostra a figura.

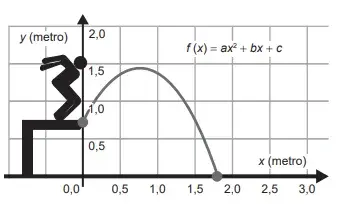
Seja D o domínio da função f (x), como definida na figura.

Para que a situação representada na figura seja real, o domínio dessa função deve ser igual a

1. {X2}, sendo x2 a raiz positiva de f (x).
2. {X ∈ ℝ | 0 ≤ X ≤ X2}, sendo x2 a raiz positiva de f (x).
3. {X ∈ ℝ | X1 ≤ X ≤ X2}, sendo x1 e x2 raízes de f (x), com x1 < x2.
4. {X ∈ ℝ | X ≥ 0}
5. X ∈ ℝ.

09. (Enem Libras 2017) Suponha que para um trem trafegar de uma cidade à outra seja necessária a construção de um túnel com altura e largura iguais a 10 m. Por questões relacionadas ao tipo de solo a ser escavado, o túnel deverá ser tal que qualquer seção transversal seja o arco de uma determinada parábola, como apresentado na Figura 1. Deseja-se saber qual a equação da parábola que contém esse arco. Considere um plano cartesiano com centro no ponto médio da base da abertura do túnel, conforme Figura 2.

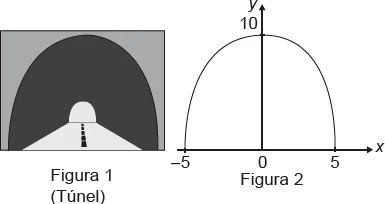
A equação que descreve a parábola é