Ponto Médio e Baricentro

01. (EEAR) Seja ABC um triângulo tal que A(1, 1), B(3, –1) e C(5, 3). O ponto ______ é o baricentro desse triângulo.

1. (2, 1)
2. (3, 3)
3. (1, 3)
4. (3, 1)

02. (FGV-RJ) Considere a circunferência de centro na origem e raio R e os pontos A(R, 0) e B(−R, 0).

Quando um ponto C pertencente a essa circunferência a percorre completamente, o baricentro do triângulo ABC descreve uma curva fechada.

A área limitada por essa curva descrita pelo baricentro do triângulo ABC é

1. πR²/4
2. πR²/3
3. πR²
4. πR²/2
5. πR²/9

03. (UEA) Seja D o ponto médio do lado BC do triângulo ABC, conforme a figura.

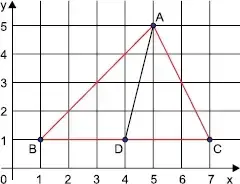
O comprimento da mediana AD é

1. √11
2. √13
3. √15
4. √17
5. √19

04. (UFRR) Uma reta r passa pelas interseções das circunferências dadas pelas equações: x² + y² + 2x + 2y - 3 = 0 e x² + y² - x - 4y - 3 = 0.

Determine a equação da reta perpendicular a r que passa pelo ponto médio do segmento que liga as interseções das circunferências.

1. y = 1/5 + 2 (x + 2/5)
2. y = 1/5 - 2 (x + 2/5)
3. y = 2/5 + 2 (x + 1/5)
4. y = 1/5 + 2 (x - 1/5)
5. y = 2/5 - 2 (x - 1/5)

05. (Unimontes) Considere a ∈ IR, com a > 1. Se M(1,3) é o ponto médio do segmento de reta de extremidades A(a,4) e B(−1,2), então o valor de a é

1. 2.
2. 3.
3. 4.
4. 5.

06. (IFRS) A equação da reta perpendicular ao segmento de reta de extremos A(-2,5) e B(6,-1) e que passa pelo ponto médio desse segmento é

1. y = - 3/4 x + 7/2
2. y = -2x - 1
3. y = 4/3 x - 2/3
4. y = 8x - 6
5. y = -3x - 5

07. (ESA) Dados três pontos colineares A(x, 8), B(-3, y) e M(3, 5), determine o valor de x + y, sabendo que M é ponto médio de AB

1. 3
2. 11
3. 9
4. - 2,5
5. 5

08. (UFMS) Em um condomínio fechado da cidade de Dourados-MS, a portaria fica nas coordenadas (0, 0). O morador A, que se encontra nas coordenadas (– 3, 4), e o morador B (5, 10) pretendem se encontrar no ponto médio entre suas localidades.

Qual é o valor numérico do ponto de encontro à portaria?

1. 5.
2. 5√2.
3. 8.
4. 10.
5. 5√5

09. (UERN) Seja M o ponto médio do segmento de reta AB, tal que A(3, 4) e B(7, 8) e N o ponto médio dos segmentos OP e MB. Sendo P(13, 13), a distância entre os pontos A e O, em unidades, é:

1. 3.
2. 4.
3. 5.
4. 6.

10. (UEA) Em um sistema de coordenadas cartesianas ortogonais estão representados uma circunferência de centro M, que passa pelo ponto O(0, 0), e um triângulo retângulo ABC, cujos vértices são determinados pelos pontos A(1,1), B(1,3) e C(3,1), conforme figura.

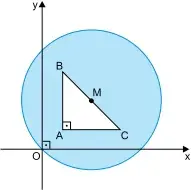
Sendo M o ponto médio do segmento BC, a área da região destacada em azul na figura é igual a

1. 2(3π – 1).
2. 10π.
3. 2(4π – 1).
4. 6π.
5. 8π.

11. (UNICAMP) No plano cartesiano, a reta de equação 2x – 3y = 12 intercepta os eixos coordenados nos pontos A e B. O ponto médio do segmento AB tem coordenadas

1. (4, 4/3).
2. (3, 2).
3. (4, –4/3).
4. (3, –2).

12. (UDESC) Sejam A(1,a) B(b,3), C(4,6) e D(1,5) os vértices de um paralelogramo e M (5/2, 4) o ponto médio da diagonal AC. O produto a · b é igual a:

1. 6
2. 2
3. 4
4. 5
5. 8

13. (ESPM) Considere no plano cartesiano os pontos A(1, 2), B(–5, 5) e C(3, 7). Seja P um ponto do segmento AB tal que AP = 2 · PB e seja M o ponto médio de BC. A equação reduzida da reta que passa por P e M é:

1. y = 2x + 8
2. y = x + 7
3. y = –2x + 4
4. y = –x + 5
5. y = 3x + 9

14. (URCA) Sendo M1=( 6,4), M2=(7,1) e M3=(2,0) as coordenadas dos pontos médios dos vértices de um triângulo, podemos afirmar que a área deste triângulo vale:

1. 76 u. a.
2. 64 u.a.
3. 52u .a .
4. 46u. a.
5. 32u .a .

15. (UESB) Considerando-se M(3, 2) ponto médio da corda AB da circunferência de equação (x − 2 )2 + y2 = 16, é correto afirmar que a distância, em unidade de comprimento, entre os pontos A e B é igual a

1. √11
2. 2√11
3. 3√11
4. 11
5. 22