Razões Trigonométricas

01. (Cesgranrio) Uma rampa plana, de 36 m de comprimento, faz ângulo de 30° com o plano horizontal. Uma pessoa que sobe a rampa inteira eleva-se verticalmente de:

1. 6√3 m.
2. 12 m.
3. 13,6 m.
4. 9√3 m.
5. 18 m.

02. (UFAM) Se um cateto e a hipotenusa de um triângulo retângulo medem 2a e 4a, respectivamente, então a tangente do ângulo oposto ao menor lado é:

1. 2√3
2. $\frac{\mathrm{\surd 3}}{3}$
3. $\frac{\mathrm{\surd 3}}{6}$
4. $\frac{\mathrm{\surd 20}}{\mathrm{20}}$
5. 3√3

03. (Cesgranrio) Uma escada de 2m de comprimento está apoiada no chão e em uma parede vertical. Se a escada faz 30° com a horizontal, a distância do topo da escada ao chão é de:

1. 0,5 m
2. 1 m
3. 1,5 m
4. 1,7 m
5. 2 m

04. (UFJF) A uma tela de computador está associado um sistema de coordenadas cartesianas, com origem no canto inferior esquerdo. Um certo programa gráfico pode ser usado para desenhar na tela somente retas de inclinações iguais a 0°, 30°, 45°, 60° e 90° em relação ao eixo horizontal. Então, considerando-se os pontos a seguir, o único que não pode estar sobre uma reta, a partir da origem, desenhada por este programa é:

1. (0, 10√3)
2. (10√3)
3. (10√3, 10√3)
4. (10√3, 5√3) x
5. (10√3, 5)

05. (Ufes) Duas circunferências são tangentes entre si e aos lados de um ângulo. Se R é o raio da maior, r é o raio da menor e o ângulo mede 60°, então

1. R = (3√3)r/2
2. R = 2√3r
3. R = 3√3r
4. R = 2r
5. R = 3r

06. (Enem 2009) Ao morrer, o pai de João, Pedro e José deixou como herança um terreno retangular de 3 km x 2 km que contém uma área de extração de ouro delimitada por um quarto de círculo de raio 1 km a partir do canto inferior esquerdo da propriedade. Dado o maior valor da área de extração de ouro, os irmãos acordaram em repartir a propriedade de modo que cada um ficasse com a terça parte da área de extração, conforme mostra a figura.

Terreno retangular e sua divisão (Foto: Reprodução/ENEM)

Em relação à partilha proposta, constata-se que a porcentagem da área do terreno que coube a João corresponde, aproximadamente, a

(considere $\frac{\mathrm{\surd 3}}{3}$ = 0,58)

1. 50%.
2. 43%.
3. 37%.
4. 33%.
5. 19%.

07. (UFAM) Apenas três degraus dão acesso à porta de uma escola, sendo que cada um tem 20 cm de altura. Para atender portadores de necessidades especiais, será construída uma rampa respeitando a legislação em vigor. A rampa deve formar, com o solo, um ângulo de 6°, conforme mostra a figura a seguir.

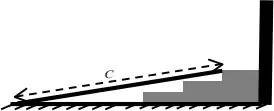
O comprimento C desta rampa em metros será aproximadamente de:

Dados: sen 6° ≈ 0,1045, cos 6° ≈ 0,9945

1. 5,57
2. 5,74
3. 6,53
4. 8,26
5. 8,84

08. (FGV-SP) Um edifício comercial tem 48 salas, distribuídas em 8 andares, conforme indica a figura. O edifício foi feito em um terreno cuja inclinação em relação à horizontal mede α graus. A altura de cada sala é 3 m, a extensão 10 m, e a altura da pilastra de sustentação, que mantém o edifício na horizontal, é 6 m.

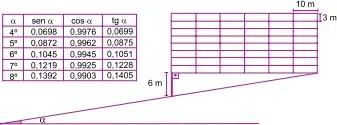
Usando os dados da tabela, a melhor aproximação inteira para α é

1. 4°
2. 5°
3. 6°
4. 7°
5. 8°

09. (UPE) No triângulo SRT, representado a seguir, os lados RT e RS tem medidas iguais. Sabendo que o segmento RU mede 6 cm e o segmento ST mede 8√2 cm, a área do triângulo SRU é quantos por cento da área do triângulo SRT?

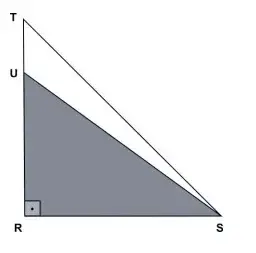
1. 60%
2. 70%
3. 75%
4. 80%
5. 85%

10. (PUC-PR) No triângulo retângulo representado na figura a seguir, determine a medida de x considerando sen 40º = 0,64:

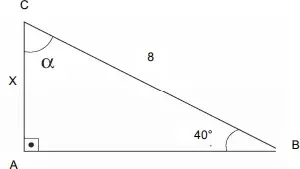
1. 3,2
2. 4,88
3. 5,12
4. 6.8
5. 2,56

11. (UECE) A medida do cosseno do maior dos ângulos internos do triângulo cujas medidas dos lados são respectivamente 8 m, 10 m e 15 m é igual a

1. - 0,38125.
2. - 0,42112.
3. - 0,43713.
4. - 0,46812.

12. (UFN)

Uma telha, na entrada do restaurante, quebrou. Em dias chuvosos, uma goteira produz no chão, embaixo da telha quebrada, uma pequena poça d'água, a 0,95 m de uma das paredes da entrada do restaurante, conforme mostra a figura abaixo.

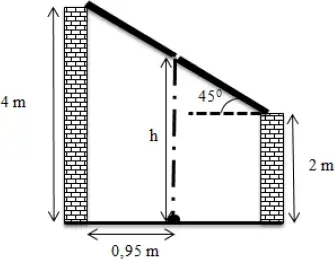
Desconsiderando a espessura do telhado, a altura (h), em metros, da telha quebrada ao chão é

1. 3,05.
2. 3,10.
3. 3,15.
4. 3,20.
5. 3,25.

13. (PUC-PR) Um determinado professor de uma das disciplinas do curso de Engenharia Civil da PUC solicitou como trabalho prático que um grupo de alunos deveria efetuar a medição da altura da fachada da Biblioteca Central da PUC usando um teodolito. Para executar o trabalho e determinar a altura, eles colocaram um teodolito a 6 metros da base da fachada e mediram o ângulo, obtendo 30º, conforme mostra figura abaixo.

Se a luneta do teodolito está a 1,70m do solo, qual é, aproximadamente, a altura da fachada da Biblioteca Central da PUC?

Dados (sen 30º = 0,5, cos 30º = 0,87 e tg 30º = 0,58)

1. 5,18 m.
2. 4,70 m.
3. 5,22 m.
4. 5,11 m.
5. 5,15 m.

14. (UERJ) O raio de uma roda gigante de centro C mede CA = CB = 10 m. Do centro C ao plano horizontal do chão, há uma distância de 11 m. Os pontos A e B, situados no mesmo plano vertical, ACB, pertencem à circunferência dessa roda e distam, respectivamente, 16 m e 3,95 m do plano do chão. Observe o esquema e a tabela:

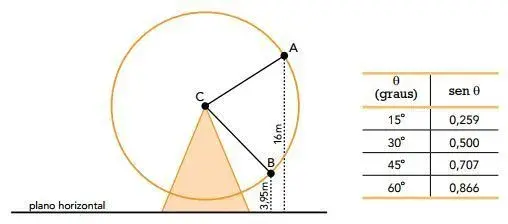
A medida, em graus, mais próxima do menor ângulo ACB corresponde a:

1. 45
2. 60
3. 75
4. 105

15. (UECE) Seja AEC um triângulo isósceles (as medidas dos lados AE e AC são iguais) e O um ponto do lado AC tal que a medida do ângulo EÔC é 120 graus. Se existe um ponto B, do lado AE, tal que o segmento OB é perpendicular ao lado AE e a medida do ângulo EÔB seja igual a 40 graus, então a medida do ângulo OÊC, em graus, é igual a

1. 9.
2. 7.
3. 5.
4. 3.