Razão, Proporção e Porcentagem: V

1. (Enem 2013) Um comerciante visita um centro de vendas para fazer cotação de preços dos produtos que deseja comprar. Verifica que se aproveita 100% da quantidade adquirida de produtos do tipo A, mas apenas 90% de produtos do tipo B. Esse comerciante deseja comprar uma quantidade de produtos, obtendo o menor custo/benefı́cio em cada um deles. O quadro mostra o preço por quilograma, em reais, de cada produto comercializado.

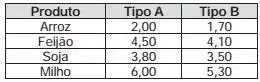
Os tipos de arroz, feijão, soja e milho que devem ser escolhidos pelo comerciante são, respectivamente,

1. A, A, A, A.
2. A, B, A, B.
3. A, B, B, A.
4. B, A, A, B.
5. B, B, B, B.

2. (Enem 2013) Uma torneira não foi fechada corretamente e fiou pingando, da meia-noite às seis horas da manhã, com a frequência de uma gota a cada três segundos. Sabe-se que cada gota d’agua tem volume de 0,2 mL.

Qual foi o valor mais aproximado do total de água desperdiçada nesse perı́odo, em litros?

1. 0,2
2. 1,2
3. 1,4
4. 12,9
5. 64,8

3. (Enem 2012) A cerâmica possui a propriedade da contração, que consiste na evaporação da água existente em um conjunto ou bloco cerâmico submetido a uma determinada temperatura elevada: em seu lugar aparecendo “espaços vazios”que tendem a se aproximar. No lugar antes ocupado pela água vão fiando lacunas e, consequentemente, o conjunto tende a retrair-se. Considere que no processo de cozimento a cerâmica de argila sofra uma contração, em dimensões lineares, de 20%.

Disponı́vel em: www.arq.ufsc.br. Acesso em: 30 mar. 2012 (adaptado).

Levando em consideração o processo de cozimento e a contração sofrida, o volume V de uma travessa de argila, de forma cúbica de aresta a, diminui para um valor que é

1. 20% menor que V , uma vez que o volume do cubo é diretamente proporcional ao comprimento de seu lado.
2. 36% menor que V , porque a área da base diminui de a 2 para ((1 − 0, 2)a)².
3. 48,8% menor que V , porque o volume diminui de a 3 para (0, 8a)³.
4. 51,2% menor que V , porque cada lado diminui para 80% do comprimento original.
5. 60% menor que V , porque cada lado diminui 20%.

4. (Enem 2012) Um laboratório realiza exames em que é possı́vel observar a taxa de glicose de uma pessoa. Os resultados são analisados de acordo com o quadro a seguir.

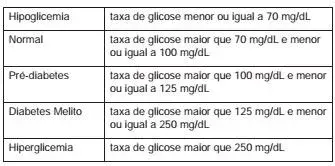
Um paciente fez um exame de glicose nesse laboratório e comprovou que estava com hiperglicemia. Sua taxa de glicose era de 300 mg/dL. Seu médico prescreveu um tratamento em duas etapas. Na primeira etapa ele conseguiu reduzir sua taxa em 30% e na segunda etapa em 10%. Ao calcular sua taxa de glicose após as duas reduções, o paciente verificou que estava na categoria de

1. hipoglicemia.
2. normal.
3. pré-diabetes.
4. diabetes melito.
5. hiperglicemia.

5. (Enem 2012) Há, em virtude da demanda crescente de economia de água, equipamentos e utensı́lios como, por exemplo, as bacias sanitárias ecológicas, que utilizam 6 litros de água por descarga em vez dos 15 litros utilizados por bacias sanitárias não ecológicas, conforme dados da Associação Brasileira de Normas Técnicas (ABNT).

Qual será a economia diária de água obtida por meio da substituição de uma bacia sanitária não ecológica, que gasta cerca de 60 litros por dia com a descarga, por uma bacia sanitária ecológica?

1. 24 litros
2. 36 litros
3. 40 litros
4. 42 litros
5. 50 litros

6. (Enem 2012) Nos shopping centers costumam existir parques com vários brinquedos e jogos. Os usuários colocam créditos em um cartão, que são descontados por cada perı́odo de tempo de uso dos jogos. Dependendo da pontuação da criança no jogo, ela recebe um certo número de tı́quetes para trocar por produtos nas lojas dos parques. Suponha que o perı́odo de uso de um brinquedo em certo shopping custa R$ 3,00 e que uma bicicleta custa 9 200 tı́quetes. Para uma criança que recebe 20 tı́quetes por perı́odo de tempo que joga, o valor, em reais, gasto com créditos para obter a quantidade de tı́quetes para trocar pela bicicleta é

1. 153.
2. 460.
3. 1 218.
4. 1 380.
5. 3 066.

7. (Enem 2012) Uma mãe recorreu à bula para verificar a dosagem de um remédio que precisava dar a seu filho. Na bula, recomendava-se a seguinte dosagem: 5 gotas para cada 2 kg de massa corporal a cada 8 horas.

Se a mãe ministrou corretamente 30 gotas do remédio a seu filho a cada 8 horas, então a massa corporal dele é de

1. 12 kg
2. 16 kg.
3. 24 kg.
4. 36 kg.
5. 75 kg.

8. (Enem 2012) Os hidrômetros são marcadores de consumo de água em residências e estabelecimentos comerciais. Existem vários modelos de mostradores de hidrômetros, sendo que alguns deles possuem uma combinação de um mostrador e dois relógios de ponteiro. O número formado pelos quatro primeiros algarismos do mostrador fornece o consumo em m³, e os dois últimos algarismos representam, respectivamente, as centenas e dezenas de litros de água consumidos. Um dos relógios de ponteiros indica a quantidade em litros, e o outro em décimos de litros, conforme ilustrados na figura a seguir.

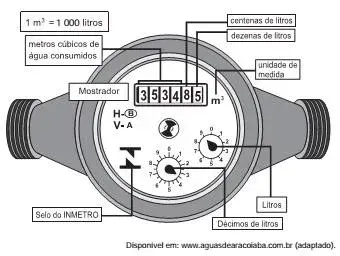
Considerando as informações indicadas na figura, o consumo total de água registrado nesse hidrômetro, em litros, é igual a

1. 3 534,85.
2. 3 544,20.
3. 3 534 850,00.
4. 3 534 859,35.
5. 3 534 850,39.

9. (Enem 2012) Um biólogo mediu a altura de cinco árvores distintas e representou-as em uma mesma malha quadriculada, utilizando escalas diferentes, conforme indicações na figura a seguir.

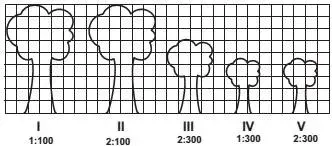
Qual é a árvore que apresenta a maior altura real?

1. I
2. II
3. III
4. IV
5. V

10. (Enem 2012) A capacidade mı́nima, em BTU/h, de um aparelho de ar-condicionado, para ambientes sem exposição ao sol, pode ser determinada da seguinte forma:

• 600BT U/h por m 2, considerando-se até duas pessoas no ambiente;

• para cada pessoa adicional nesse ambiente, acrescentar 600BT U/h;

• acrescentar mais 600BT U/h para cada equipamento eletroeletrônico em funcionamento no ambiente.

Será instalado um aparelho de ar-condicionado em uma sala, sem exposição ao sol, de dimensões 4m × 5m, em que permaneçam quatro pessoas e possua um aparelho de televisão em funcionamento.

A capacidade mı́nima, em BT U/h, desse aparelho de arcondicionado deve ser

1. 12 000.
2. 12 600.
3. 13 200.
4. 13 800.
5. 15 000.

11. (Enem 2012) Arthur deseja comprar um terreno de Cléber, que lhe oferece as seguintes possibilidades de pagamento:

• Opção 1: Pagar à vista, por R$ 55 000,00;

• Opção 2: Pagar a prazo, dando uma entrada de R$ 30 000,00, e mais uma prestação de R$ 26 000,00 para dali a 6 meses.

• Opção 3: Pagar a prazo, dando uma entrada de R$ 20 000,00, mais uma prestação de R$ 20 000,00, para dali a 6 meses e outra de R$ 18 000,00 para dali a 12 meses da data da compra.

• Opção 4: Pagar a prazo dando uma entrada de R$ 15 000,00 e o restante em 1 ano da data da compra, pagando R$ 39 000,00.

• Opção 5: pagar a prazo, dali a um ano, o valor de R$ 60 000,00.

Arthur tem o dinheiro para pagar à vista, mas avalia se não seria melhor aplicar o dinheiro do valor à vista (ou até um valor menor) em um investimento, com rentabilidade de 10% ao semestre, resgatando os valores à medida que as prestações da opção escolhida fossem vencendo. Após avaliar a situação do ponto de vista financeiro e das condições apresentadas, Arthur concluiu que era mais vantajoso financeiramente escolher a opção

1. 1
2. 2
3. 3
4. 4
5. 5

12. (Enem 2012) José, Carlos e Paulo devem transportar em suas bicicletas uma certa quantidade de laranjas. Decidiram dividir o trajeto a ser percorrido em duas partes, sendo que ao final da primeira parte eles redistribuiriam a quantidade de laranjas que cada um carregava dependendo do cansaço de cada um. Na primeira parte do trajeto José, Carlos e Paulo dividiram as laranjas na proporção 6 : 5 : 4, respectivamente. Na segunda parte do trajeto José, Carlos e Paulo dividiram as laranjas na proporção 4 : 4 : 2, respectivamente.

Sabendo-se que um deles levou 50 laranjas a mais no segundo trajeto, qual a quantidade de laranjas que José, Carlos e Paulo, nessa ordem, transportaram na segunda parte do trajeto?

1. 600, 550, 350
2. 300, 300, 150
3. 300, 250, 200
4. 200, 200, 100
5. 100, 100, 50

13. (Enem 2012) O esporte de alta competição da atualidade produziu uma questão ainda sem resposta: Qual é o limite do corpo humano? O maratonista original, o grego da lenda, morreu de fadiga por ter corrido 42 quilômetros. O americano Dean Karnazes, cruzando sozinho as planı́cies da Califórnia, conseguiu correr dez vezes mais em 75 horas.

Um professor de Educação Fı́sica, ao discutir com a turma o texto sobre a capacidade do maratonista americano, desenhou na lousa uma pista reta de 60 centı́metros, que representaria o percurso referido.

Disponı́vel em: http://veja.abril.com.br. Acesso em: 25 jun. 2011 (adaptado).

Se o percurso de Dean Karnazes fosse também em uma pista reta, qual seria a escala entre a pista feita pelo professor e a percorrida pelo atleta?

1. 1:700
2. 1:7 000
3. 1:70 000
4. 1:700 000
5. 1:7 000 000

14. (Enem 2011) Um jovem investidor precisa escolher qual investimento lhe trará maior retorno financeiro em uma aplicação de R$ 500,00. Para isso, pesquisa o rendimento e o imposto a ser pago em dois investimentos: poupança e CDB (certificado de depósito bancário). As informações obtidas estão resumidas no quadro:

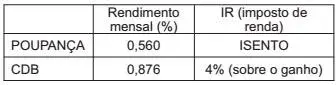
Para o jovem investidor, ao final de um mês, a aplicação mais vantajosa é

1. a poupança, pois totalizará um montante de R$ 502,80.
2. a poupança, pois totalizará um montante de R$ 500,56.
3. o CDB, pois totalizará um montante de R$ 504,38.
4. o CDB, pois totalizará um montante de R$ 504,21.
5. o CDB, pois totalizará um montante de R$ 500,87.

15. (Enem 2011) Observe as dicas para calcular a quantidade certa de alimentos e bebidas para as festas de fim de ano:

- Para o prato principal, estime 250 gramas de carne para cada pessoa.

- Um copo americano cheio de arroz rende o suficiente para quatro pessoas.

- Para a farofa, calcule quatro colheres de sopa por convidado.

- Uma garrafa de vinho serve seis pessoas.

- Uma garrafa de cerveja serve duas.

- Uma garrafa de espumante serve três convidados.

Quem organiza festas faz esses cálculos em cima do total de convidados, independente do gosto de cada um.

Um anfitrião decidiu seguir essas dicas ao se preparar para receber 30 convidados para a ceia de Natal. Para seguir essas orientações à risca, o anfitrião deverá dispor de

1. 120 kg de carne, 7 copos americanos e meio de arroz, 120 colheres de sopa de farofa, 5 garrafas de vinho, 15 de cerveja e 10 de espumante.
2. 120 kg de carne, 7 copos americanos e meio de arroz, 120 colheres de sopa de farofa, 5 garrafas de vinho, 30 de cerveja e 10 de espumante.
3. 75 kg de carne, 7 copos americanos e meio de arroz, 120 colheres de sopa de farofa, 5 garrafas de vinho, 15 de cerveja e 10 de espumante.
4. 7,5 kg de carne, 7 copos americanos de arroz, 120 colheres de sopa de farofa, 5 garrafas de vinho, 30 de cerveja e 10 de espumante.
5. 7,5 kg de carne, 7 copos americanos e meio de arroz, 120 colheres de sopa de farofa, 5 garrafas de vinho, 15 de cerveja e 10 de espumante.

16. (Enem 2011) A participação dos estudantes na Olimpı́ada Brasileira de Matemática das Escolas Públicas (OBMEP) aumenta a cada ano. O quadro indica o percentual de medalhistas de ouro, por região, nas edições da OBMEP de 2005 a 2009.

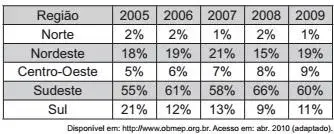
Em relação às edições de 2005 a 2009 da OBMEP, qual o percentual médio de medalhistas de ouro da região Nordeste?

1. 14,6%
2. 18,2%
3. 18,4%
4. 19,0%
5. 21,0%

17. (Enem 2011) O Índice de Massa Corporal (IMC) é largamente utilizado há cerca de 200 anos, mas esse cálculo representa muito mais a corpulência que a adiposidade uma vez que indivı́duos musculosos e obesos podem apresentar o mesmo IMC. Uma nova pesquisa aponta o Índice de Adiposidade Corporal (IAC) como uma alternativa mais fidedigna para quantificar a gordura corporal, utilizando a medida do quadril e a altura. A figura mostra como calcular essas medidas, sabendo-se que, em mulheres, a adiposidade normal está entre 19% e 26%.

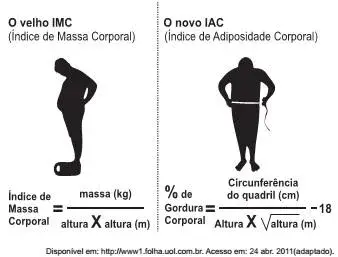
Uma jovem com IMC = 20kg/m², 100 cm de circunferência dos quadris e 60 kg de massa corpórea resolveu averiguar seu IAC. Para se enquadrar aos nı́veis de normalidade de gordura corporal, a atitude adequada que essa jovem deve √ ter diante da nova medida é (Use raiz √3 = 1,7 e raiz √1,7 = 1, 3)

1. reduzir seu excesso de gordura em cerca de 1%.
2. reduzir seu excesso de gordura em cerca de 27%.
3. manter seus nı́veis atuais de gordura.
4. aumentar seu nı́vel de gordura em cerca de 1%.
5. aumentar seu nı́vel de gordura em cerca de 27%.

18. (Enem 2011) Em 2010, um caos aéreo afetou o continente europeu, devido à quantidade de fumaça expelida por um vulcão na Islândia, o que levou ao cancelamento de inúmeros voos.

Cinco dias após o inı́cio desse caos, todo o espaço aéreo europeu acima de 6 000 metros estava liberado, com exceção do espaço aéreo da Finlândia. Lá, apenas voos internacionais acima de 31 mil pés estavam liberados.

Disponı́vel em: http://www1.folha.uol.com.br. Acesso em: 21 abr. 2010 (adaptado).

Considere que 1 metro equivale a aproximadamente 3,3 pés.

Qual a diferença, em pés, entre as altitudes liberadas na Finlândia e no restante do continente europeu cinco dias após o inı́cio do caos?

1. 3 390 pés.
2. 9 390 pés.
3. 11 200 pés.
4. 19 800 pés.
5. 50 800 pés.

19. (Enem 2011) Sabe-se que a distância real, em linha reta, de uma cidade A, localizada no estado de São Paulo, a uma cidade B, localizada no estado de Alagoas, é igual a 2 000 km. Um estudante, ao analisar um mapa, verificou com sua régua que a distância entre essas duas cidades, A e B, era 8 cm.

Os dados nos indicam que o mapa observado pelo estudante está na escala de

1. 1 : 250
2. 1 : 2 500
3. 1 : 25 000
4. 1 : 250 000
5. 1 : 25 000 000

20. (Enem 2011) Café no Brasil

O consumo atingiu o maior nı́vel da história no ano passado: os brasileiros beberam o equivalente a 331 bilhões de xı́caras.

Veja. Ed. 2158, 31 mar. 2010.

Considere que a xı́cara citada na notı́cia seja equivalente a, aproximadamente, 120 mL de café. Suponha que em 2010 os brasileiros bebam ainda mais café, aumentando o consumo em $\frac{1}{5}$ do que foi consumido no ano anterior. De acordo com essas informações, qual a previsão mais aproximada para o consumo de café em 2010?

1. 8 bilhões de litros.
2. 16 bilhões de litros.
3. 32 bilhões de litros.
4. 40 bilhões de litros.
5. 48 bilhões de litros.

21. (Enem 2011) Para uma atividade realizada no laboratório de Matemática, um aluno precisa construir uma maquete da quadra de esportes da escola que tem 28 m de comprimento por 12 m de largura. A maquete deverá ser construı́da na escala de 1 : 250.

Que medida de comprimento e largura, em cm, o aluno utilizará na construção da maquete?

1. 4,8 e 11,2
2. 7,0 e 3,0
3. 11,2 e 4,8
4. 28,0 e 12,0
5. 30,0 e 70,0

22. (Enem 2011) Você pode adaptar as atividades do seu dia a dia de uma forma que possa queimar mais calorias do que as gastas normalmente, conforme a relação seguinte:

- Enquanto você fala ao telefone, faça agachamentos: 100 calorias gastas em 20 minutos.

- Meia hora de supermercado: 100 calorias.

- Cuidar do jardim por 30 minutos: 200 calorias.

- Passear com o cachorro: 200 calorias em 30 minutos.

- Tirar o pó dos móveis: 150 calorias em 30 minutos.

- Lavar roupas por 30 minutos: 200 calorias.

Disponı́vel em: http://cyberdiet.terra.com.br. Acesso em: 27 abr. 2010 (adaptado).

Uma pessoa deseja executar essas atividades, porém, ajustando o tempo para que, em cada uma, gaste igualmente 200 calorias.

A partir dos ajustes, quanto tempo a mais será necessário para realizar todas as atividades?

1. 50 minutos.
2. 60 minutos.
3. 80 minutos.
4. 120 minutos.
5. 170 minutos.

23. (Enem 2010) O Salto Triplo é uma modalidade do atletismo em que o atleta dá um salto em um só pé, uma passada e um salto, nessa ordem. Sendo que o salto com impulsão em um só pé será feito de modo que o atleta caia primeiro sobre o mesmo pé que deu a impulsão; na passada ele cairá com o outro pé, do qual o salto é realizado.

Disponı́vel em: www.cbat.org.br (adaptado).

Um atleta da modalidade Salto Triplo, depois de estudar seus movimentos, percebeu que, do segundo para o primeiro salto, o alcance diminuı́a em 1,2 m, e, do terceiro para o segundo salto, o alcance diminuı́a 1,5 m. Querendo atingir a meta de 17,4 m nessa prova e considerando os seus estudos, a distância alcançada no primeiro salto teria de estar entre

1. 4,0 m e 5,0 m.
2. 5,0 m e 6,0 m.
3. 6,0 m e 7,0 m.
4. 7,0 m e 8,0 m.
5. 8,0 m e 9,0 m.

24. (Enem 2010) Embora o Índice de Massa Corporal (IMC) seja amplamente utilizado, existem ainda inúmeras restrições teóricas ao uso e às faixas de normalidade preconizadas. O Recı́proco do Índice Ponderal (RIP), de acordo com o modelo alométrico, possui uma melhor fundamentação matemática, já que a massa é uma variável de dimensões cúbicas e a altura, uma variável de dimensões lineares. As fórmulas que determinam esses ı́ndices são:

Se uma menina, com 64 kg de massa, apresenta IMC igual a 25kg/m², então ela possui RIP igual a

1. 0,4cm/kg^1/3.
2. 2,5cm/kg^1/3.
3. 8cm/kg^1/3.
4. 20cm/kg^1/3.
5. 40cm/kg^1/3.

25. (Enem 2010) Uma empresa possui um sistema de controle de qualidade que classifica o seu desempenho financeiro anual, tendo como base o do ano anterior. Os conceitos são: insuficiente, quando o crescimento é menor que 1%; regular, quando o crescimento é maior ou igual a 1% e menor que 5%; bom, quando o crescimento é maior ou igual a 5% e menor que 10%; ótimo, quando é maior ou igual a 10% e menor que 20%; e excelente, quando é maior ou igual a 20%. Essa empresa apresentou lucro de R$ 132 000,00 em 2008 e de R$ 145 000,00 em 2009.

De acordo com esse sistema de controle de qualidade, o desempenho financeiro dessa empresa no ano de 2009 deve ser considerado

1. insuficiente
2. regular.
3. bom.
4. ótimo.
5. excelente.