PFC

01. (Enem 2025) Ao realizar o cadastro em um aplicativo de investimentos, foi solicitado ao usuário que criasse uma senha, sendo permitido o uso somente dos seguintes caracteres:

• algarismos de 0 a 9;

• 26 letras minúsculas do alfabeto;

• 26 letras maiúsculas do alfabeto;

• 6 caracteres especiais: !, @, #, $, *, &.

Três tipos de estruturas para senha foram apresentadas ao usuário:

• tipo I: formada por quaisquer quatro caracteres distintos, escolhidos dentre os permitidos;

• tipo II: formada por cinco caracteres distintos, iniciando por três letras, seguidas por um algarismo e, ao final, um caractere especial;

• tipo III: formada por seis caracteres distintos, iniciando por duas letras, seguidas por dois algarismos e, ao final, dois caracteres especiais.

Considerando P1, P2 e P3, e as probabilidades de se descobrirem ao acaso, na primeira tentativa, as senhas dos tipos I, II e III, respectivamente.

Nessas condições, o tipo de senha que apresenta a menor probabilidade de ser descoberta ao acaso, na primeira tentativa, é

1. tipo I, pois p1 < p2 < p3.
2. tipo I, pois tem menor quantidade de caracteres.
3. tipo II, pois tem maior quantidade de letras.
4. tipo III, pois p3 < p2 < p1.
5. tipo III, pois tem maior quantidade de caracteres.

02. (Enem 2025) Uma montadora de automóveis divulgou que oferta a seus clientes mais de 1 000 configurações diferentes de carro, variando o modelo, a motorização, os opcionais e a cor do veículo. Atualmente, ela oferece 7 modelos de carros com 2 tipos de motores: 1.0 e 1.6. Já em relação aos opcionais, existem 3 escolhas possíveis: central multimídia, rodas de liga leve e bancos de couro, podendo o cliente optar por incluir um, dois, três ou nenhum dos opcionais disponíveis.

Para ser fiel à divulgação feita, a quantidade mínima de cores que a montadora deverá disponibilizar a seus clientes é

1. 8.
2. 9.
3. 11.
4. 18.
5. 24.

03. (Enem 2025) Um hotel de 3 andares está sendo construído. Cada andar terá 100 quartos. Os quartos serão numerados de 100 a 399 e cada um terá seu número afixado à porta. Cada número será composto por peças individuais, cada uma simbolizando um único algarismo.

Qual a quantidade mínima de peças, simbolizando o algarismo 2, necessárias para identificar o número de todos os quartos?

1. 160
2. 157
3. 130
4. 120
5. 60

04. (Enem Digital 2020) "1, 2, 3, GOL, 5, 6, 7, GOL, 9, 10, 11, GOL, 13, GOL, 15, GOL, 17, 18, 19, GOL, 21, 22, 23, GOL, 25, ..."

Para a Copa do Mundo de Futebol de 2014, um bar onde se reuniam amigos para assistir aos jogos criou uma brincadeira. Um dos presentes era escolhido e tinha que dizer, numa sequência em ordem crescente, os números naturais não nulos, trocando os múltiplos de 4 e os números terminados em 4 pela palavra GOL. A brincadeira acabava quando o participante errava um termo da sequência.

Um dos participantes conseguiu falar até o número 103, respeitando as regras da brincadeira.

O total de vezes em que esse participante disse a palavra GOL foi

1. 20.
2. 28.
3. 30.
4. 35.
5. 40.

05. (Enem PPL 2019) Uma pessoa comprou um aparelho sem fio para transmitir músicas a partir do seu computador para o rádio de seu quarto. Esse aparelho possui quatro chaves seletoras e cada uma pode estar na posição 0 ou 1. Cada escolha das posições dessas chaves corresponde a uma frequência diferente de transmissão.

A quantidade de frequências diferentes que esse aparelho pode transmitir é determinada por

1. 6.
2. 8.
3. 12.
4. 16.
5. 24

06. (Enem 2025) O comitê organizador da Copa do Mundo 2014 criou a logomarca da Copa, composta de uma figura plana e o slogan "Juntos num só ritmo", com mãos que se unem formando a taça Fifa. Considere que o comitê organizador resolvesse utilizar todas as cores da bandeira nacional (verde, amarelo, azul e branco) para colorir a logomarca, de forma que regiões vizinhas tenham cores diferentes.

De quantas maneiras diferentes o comitê organizador da Copa poderia pintar a logomarca com as cores citadas?

1. 15
2. 30
3. 108
4. 360
5. 972

07. (Enem 2025) Uma empresa construirá sua página na internet e espera atrair um público de aproximadamente um milhão de clientes. Para acessar essa página, será necessária uma senha com formato a ser definido pela empresa. Existem cinco opções de formato oferecidas pelo programador, descritas no quadro, em que "L" e "D" representam, respectivamente, letra maiúscula e dígito.

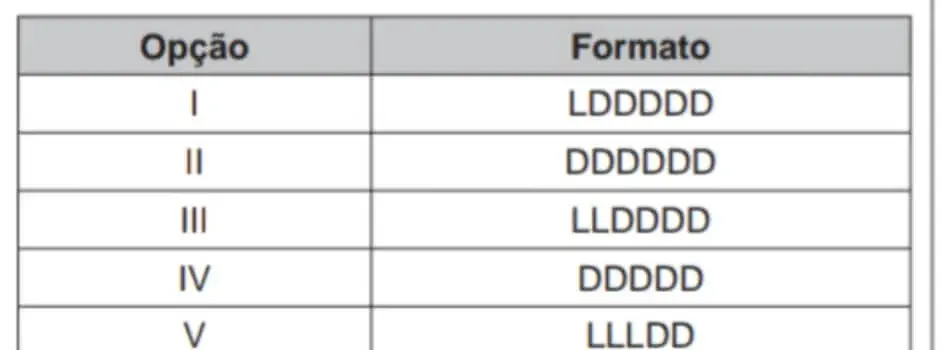
As letras do alfabeto, entre as 26 possíveis, bem como os dígitos, entre os 10 possíveis, podem se repetir em qualquer das opções.

A empresa quer escolher uma opção de formato cujo número de senhas distintas possíveis seja superior ao número esperado de clientes, mais que esse número não seja superior ao dobro do número esperado de clientes.

A opção que mais se adequa às condições da empresa é

1. I.
2. II.
3. III.
4. IV.
5. V.

08. (Enem 2025) O designer português Miguel Neiva criou um sistema de símbolos que permite que pessoas daltônicas identifiquem cores. O sistema consiste na utilização de símbolos que identificam as cores primárias (azul, amarelo e vermelho). Além disso, a justaposição de dois desses símbolos permite identificar cores secundárias (como o verde, que é o amarelo combinado com o azul). O preto e o branco são identificados por pequenos quadrados: o que simboliza o preto é cheio, enquanto o que simboliza o branco é vazio. Os símbolos que representam preto e branco também podem estar associados aos símbolos que identificam cores, significando se estas são claras ou escuras.

Folha de São Paulo. Disponível em: www1.folha.uol.com.br. Acesso em: 18 fev. 2012 (adaptado).

De acordo com o texto, quantas cores podem ser representadas pelo sistema proposto?

1. 14
2. 18
3. 20
4. 21
5. 23

09. (Enem 2025) O diretor de uma escola convidou os 280 alunos de terceiro ano a participarem de uma brincadeira. Suponha que existem 5 objetos e 6 personagens numa casa de 9 cômodos; um dos personagens esconde um dos objetos em um dos cômodos da casa. O objetivo da brincadeira é adivinhar qual objeto foi escondido por qual personagem e em qual cômodo da casa o objeto foi escondido.

Todos os alunos decidiram participar. A cada vez um aluno é sorteado e dá a sua resposta. As respostas devem ser sempre distintas das anteriores, e um mesmo aluno não pode ser sorteado mais de uma vez. Se a resposta do aluno estiver correta, ele é declarado vencedor e a brincadeira é encerrada.

O diretor sabe que algum aluno acertará a resposta porque há

1. 10 alunos a mais do que possíveis respostas distintas.
2. 20 alunos a mais do que possíveis respostas distintas.
3. 119 alunos a mais do que possíveis respostas distintas.
4. 260 alunos a mais do que possíveis respostas distintas.
5. 270 alunos a mais do que possíveis respostas distintas.