Triângulo Retângulo

01. (PUC) Em uma aula prática de Topografia, os alunos aprendiam a trabalhar com o teodolito, instrumento usado para medir ângulos. Com o auxílio desse instrumento, é possível medir a largura y de um rio. De um ponto A, o observador desloca-se 100 metros na direção do percurso do rio, e então visualiza uma árvore no ponto C, localizada na margem oposta sob um ângulo de 60°, conforme a figura abaixo.

Nessas condições, conclui-se que a largura do rio, em metros, é

1. $\frac{\mathrm{100\surd 3}}{3}$
2. $\frac{\mathrm{100\surd 3}}{2}$
3. $\mathrm{100\surd 3}$
4. $\frac{\mathrm{50\surd 3}}{3}$
5. $\mathrm{200}$

02. (FUVEST) No quadrilátero a seguir, BC = CD = 3 cm, AB = 2 cm, $A\stackrel{\wedge \; <!--\; logical\; and\; -->}{D}C$ = 60^o e $A\stackrel{\wedge \; <!--\; logical\; and\; -->}{B}C$ = 90^o.

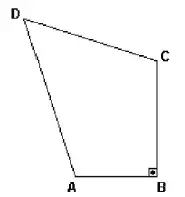
A medida da soma dos lados do quadrilátero é:

1. 11
2. 12
3. 13
4. 14
5. 15

03. (IFSP) O transporte alternativo é uma maneira de locomover-se usando um meio diferente dos mais tradicionais. A bicicleta é um exemplo disso. Em alguns lugares, ela é usada porque é mais barata, como no interior do Brasil e em países como a Índia e China. Outras pessoas escolhem andar de bicicleta por uma questão ideológica, porque elas não agridem o meio ambiente e não causam tantos transtornos quanto os carros. Usando uma bicicleta, uma pessoa sai do ponto A e dirige-se ao ponto B. O percurso, dado em km, representado pelos segmentos AC, CD e DB está esboçado no gráfico abaixo.

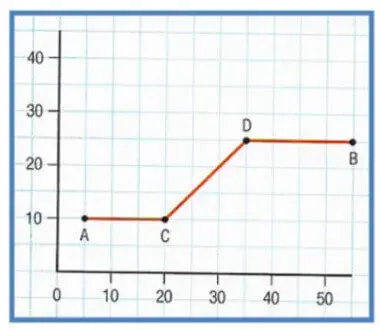
Considerando √2 = 1,4 assinale a alternativa que apresenta a distância percorrida pela pessoa do ponto A ao ponto B.

1. 56 km
2. 21 km
3. 20 km
4. 15 km
5. 10 km

4. (UEL) Um engenheiro fez um projeto para a construção de um prédio (andar térreo e mais 6 andares), no qual a diferença de altura entre o piso de um andar e o piso do andar imediatamente superior é de 3,5m. Durante a construção, foi necessária a utilização de rampas para transporte de material do chão do andar térreo até os andares superiores. Uma rampa lisa de 21m de comprimento, fazendo ângulo de 30º com o plano horizontal, foi utilizada. Uma pessoa que subir essa rampa inteira transportará material, no máximo, até o piso do:

1. 2º andar.
2. 3º andar.
3. 4º andar.
4. 5º andar.
5. 6º andar.