Equações Trigonométricas

01. (PUC) Se sen x = -1, então o valor de sen 3x é:

1. -1/3
2. 0
3. 1
4. -1
5. -3

02. (Carlos Chagas) O Número de soluções da equação cos 2x = 1/2, no intervalo [-π π], é

1. 0
2. 1
3. 2
4. 3
5. 4

03. (Fatec) O conjunto solução da equação 2cos²x+cosx-1=0, no universo U=[0,2π], é

1. {π/3, π, 5π/3}
2. {π/6, π, 5π/6}
3. {π/3, π/6, π}
4. {π/6, π/3, π, 2π/3, 5π/3}
5. {π/3, 2π/3, π, 4π/3, 5π/3, 2π}

04. (Cesgranrio) Todos os valores de x ∈ [<, 2<] que satisfazem senx.cosx>0 são:

1. π< x < 5 π/4
2. 5™/4 < x < π
3. π < x < 3π/2
4. 3π/2 < x < 2π
5. 3π/2 < x < 7π/4

05. (Ufrrj) O número de soluções da equação 2cos²x - 3cosx - 2 = 0 no intervalo [0, π] é

1. 1
2. 0
3. 2
4. 4
5. 3

06. (Unirio) O conjunto-solução da equação senx=cosx, sendo 0≤x<2π, é:

1. {π/4}
2. {π/3}
3. {5π/4}
4. {π/3, 4π/3}
5. {π/4, 5π/4}

07. (PUC-PR) Considere as expressões trigonométricas A = cos x + cos y e B = sen x – sen y.

Sabendo que x + y = 1200, assinale a alternativa que corresponde ao valor de A2 + B2.

1. 1.
2. 2.
3. 3.
4. 4.
5. 5.

08. (FGV-SP) A única solução da equação sen 2x · sen 3x = cos 2x · cos 3x, com 0° ≤ x < 90°, é

1. 72°.
2. 36°.
3. 24°.
4. 18°.
5. 15°.

09. (EEAR) No intervalo [0, π], a soma das raízes da equação 3cos²x - 7sen²x + 2 = 0 é igual a

1. 4 π
2. 3 π
3. 2 π
4. π

10. (Mackenzie) O número de soluções que a equação 4 cos2x − cos 2x + cos x = 2 admite no intervalo [0, 2π] é

1. 0
2. 1
3. 2
4. 3
5. 4

Resolução:

A partir da identidade trigonométrica cos2x = 2 cos²x – 1, pode-se reescrever a equação

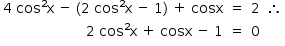
Fazendo a substituição t = cosx, chega-se a uma equação do 2º grau:

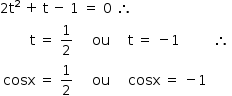
No intervalo [0, 2π], as soluções são

ou seja, 3 soluções no total.

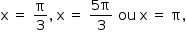
11. (UFG) Considere a equação (e^senx)² + 5 e senx – 6 = 0, na variável x. O valor inteiro de x que satisfaz a equação é

1. -6
2. 0
3. 1
4. 2
5. 3

12. (UECE) As soluções, em R, da equação cox⁴x – 4cox³x + 6cos²x – 4cosx + 1 = 0 são

1. x = 2kπ, onde k é um inteiro qualquer.
2. x = (2k + 1) π, onde k é um inteiro qualquer.
3. x = kπ, onde k é um inteiro qualquer.
4. x = (4k + 1) π, onde k é um inteiro qualquer.

13. (UPF) A quantidade de soluções que a equação trigonométrica sen⁴ x - cos⁴ x = $\frac{1}{2}$ admite no intervalo [0 , 3𝜋] é:

1. 0
2. 2
3. 4
4. 6
5. 8

14. (IME) O número de soluções da equação cos(8x) = sen(2x) + tg²(x) + cotg²(x) no intervalo [0,2π] é:

1. 0
2. 1
3. 2
4. 4
5. 8

15. (UEFS) O número de soluções da equação 3cos²x + tan²x = 3, no intervalo [0, 2π], é

1. 1
2. 2
3. 4
4. 6
5. 7

Resolução:

Como |(√3)/3 | ≤1 , existe um arco cujo cosseno dê (√3)/3 , portanto já são 4 soluções.

|cos(0)|=|cos(∏)|=|cos(2∏)|=1 (Três soluções)

No total, então, são 7 soluções.