Polígonos Regulares

1. (UFPR) Considere a seguinte sequência de polígonos regulares inscritos em um círculo de raio 2 cm:

Sabendo que a área A de um polígono regular de n lados dessa sequência pode ser calculada pela fórmula A=2n.sen(2π/n), considere as seguintes afirmativas:

1. As áreas do triângulo equilátero e do quadrado nessa sequência são, respectivamente, 3√3cm² e 8 cm².

2. O polígono regular de 12 lados, obtido nessa sequência, terá área de 12 cm².

3. À medida que n aumenta, o valor A se aproxima de 4π cm².

Assinale a alternativa correta.

1. Somente a afirmativa 1 é verdadeira.
2. Somente as afirmativas 1 e 2 são verdadeiras.
3. Somente as afirmativas 1 e 3 são verdadeiras.
4. Somente as afirmativas 2 e 3 são verdadeiras.
5. As afirmativas 1, 2 e 3 são verdadeiras.

2. (UECE) A área do polígono regular convexo circunscrito a um círculo unitário e que possui 9 diagonais é igual

1. 2√3 u. a.
2. 3√3 u. a.
3. 4√3 u. a.
4. 5√3 u. a.

3. (PUC-RS) Para uma engrenagem mecânica, deseja-se fazer uma peça de formato hexagonal regular. A distância entre os lados paralelos é de 1 cm, conforme a figura abaixo. O lado desse hexágono mede ______ cm.

1. $\frac{1}{2}$
2. $\frac{\mathrm{\surd 3}}{3}$
3. √3
4. $\frac{\mathrm{\surd 5}}{5}$
5. 1

4. (FUVEST) Uma das piscinas do Centro de Práticas Esportivas da USP tem o formato de três hexágonos regulares congruentes, justapostos, de modo que cada par de hexágonos tem um lado em comum, conforme representado na figura abaixo. A distância entre lados paralelos de cada hexágono é de 25 metros.

1. 1.600m²
2. 1.800m²
3. 2.000m²
4. 2.200m²
5. 2.400m²

5. (UECE) Se, em um polígono convexo, o número de lados n é um terço do número de diagonais, então o valor de n é:

1. 9.
2. 11.
3. 13.
4. 15.

6. (FAAP) A medida mais próxima de cada ângulo externo do heptágono regular da moeda de R$ 0,25:

1. 60°
2. 45°
3. 36°
4. 83°
5. 51°

07. (UNIFENAS) Qual é o número de diagonais que passam pelo centro de um undecágono (polígono de 11 lados) regular?

1. 44.
2. 30.
3. 20.
4. 10.
5. Nenhuma.

08. (UFRGS) A figura abaixo é formada por oito semicircunferências, cada uma com centro nos pontos médios dos lados de um octógono regular de lado 2.

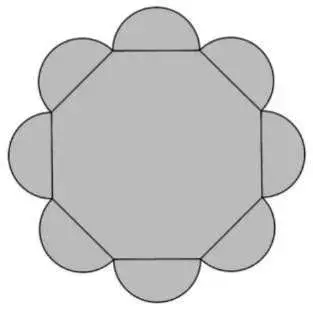
A área da região sombreada é

1. 4π + 8 + 8π2.
2. 4π + 8 + 4π2.
3. 4π + 4 + 8π2.
4. 4π + 4 + 4π2.
5. 4π + 2 + 8π2

09. (UFMS) Em geometria existem muitas simetrias, estudos dos ângulos internos e externos de uma figura. Nesse sentido, um aluno de Matemática desenhou um pentágono regular e, a partir dos seus vértices, traçou todas as diagonais. Assim, verificou a formação de uma estrela de cinco pontas, conforme a figura a seguir:

1. 1.440°.
2. 540°.
3. 180°.
4. 108°.
5. 36°.

10. (FGV-SP) Na figura, ABCDEF é um hexágono regular de lado 1 dm, e Q é o centro da circunferência inscrita a ele.

O perímetro do polígono AQCEF, em dm, é igual a

1. 4 + √2
2. 4 + √3
3. 6
4. 4 + √5
5. 2 (2 + √2)