Ângulos
Gabarito de Matemática sobre o tema Ângulos com questões de Vestibulares.
Você pode conferir as videoaulas, conteúdo de teoria, e mais questões sobre o tema Ângulos.
1. (FGV) Na figura, os pontos A e B estão no mesmo plano que contém as retas paralelas r e s. Assinale o valor de a:

- 30°
- 50°
- 40°
- 70°
- 60°
Resposta: D
Resolução:
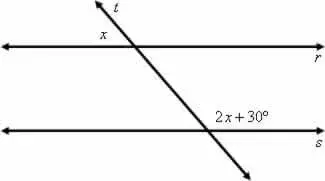
2. (FAM–SP) Dadas às retas r e s, paralelas entre si, e t, concorrente com r e s, calcule o valor de x:
- 51º
- 35º
- 90º
- 50º
- 45º
Resposta: D
Resolução: Note que o ângulo 2x + 30° é suplementar ao ângulo outro ângulo entre as retas s e t (do lado inferior direito), este mesmo ângulo e o ângulo que mede x são chamados de ângulos alternos externos, estes ângulos são congruentes, ou seja, tem o mesmo valor.
Sabendo disso, concluímos que a soma dos ângulos x e 2x + 30° é de 180°. Logo, temos:
x + 2x + 30° = 180°
3x = 150°
x = 50°
3. (ESPM) A medida de um ângulo cujo suplemento tem 100° a mais que a metade do seu complemento é igual a:
- 40°
- 50°
- 60°
- 70°
- 80°
Resposta: D
Resolução:
4. (Uniube–MG) Na figura abaixo, as retas r e s são paralelas, cortadas por uma transversal t. Se a medida do ângulo α é o triplo da medida do ângulo β, então a diferença α – β vale:
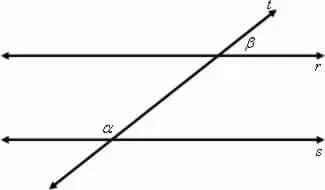
- 90º
- 85º
- 80º
- 75º
- 60º
Resposta: A
Resolução: 90º
5. (UFSE) A medida do suplemento de um ângulo é o triplo da medida do ângulo. Nessas condições, o:
- maior desses ângulos mede 140°
- maior desses ângulos mede 135°
- maior desses ângulos mede 120°.
- menor desses ângulos mede 50°.
- menor desses ângulos mede 40°.
Resposta: B
Resolução: Suplemento = 180° - x
180° - x = 3x
180° = 4x
x = 180°/4
x = 45°
180° - 45° = 135°
6. (UEL) Na figura a seguir, as medidas x, y e z são diretamente proporcionais aos números 5, 20 e 25, respectivamente.
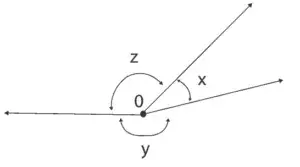
O suplemento do ângulo de medida x tem medida igual a
- 144°
- 128°
- 116°
- 82°
- 54°.
Resposta: A
Resolução:
07. (UERJ) Física
Colho esta luz solar à minha volta,
No meu prisma a disperso e recomponho:
Rumor de sete cores, silêncio branco.
JOSÉ SARAMAGO
Na imagem a seguir, o triângulo ABC representa uma seção plana paralela à base de um prisma reto. As retas n e n’ são perpendiculares aos lados AC e AB , respectivamente, e BÂC = 80°.
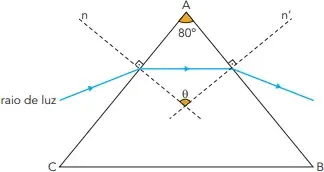
A medida do ângulo θ entre n e n’ é:
- 90º
- 100º
- 110º
- 120º
Resposta: B
Resolução:
08. (FIP-Moc) Uma hora após nascer, o sol emite um feixe de raios luminosos que atinge a superfície de um reservatório de água (idealmente plano e polido), conforme mostra a figura:

Os ângulos α e β formados pelo feixe são suplementares, e o menor corresponde a 40% do maior.
Nas condições apresentadas, o ângulo α mede, aproximadamente,
- 43º
- 47º
- 63º
- 59º
- 51º
Resposta: E
Resolução: 51º
09. (SLMANDIC) A soma dos complementos de dois ângulos é 130º e a diferença entre seus suplementos é 10º. Estes ângulos medem
- 15º e 40º.
- 18º e 35º.
- 20º e 30º.
- 25º e 40º.
- 30º e 50º.
Resposta: C
Resolução: Primeiro vamos rever os conceitos de ângulos complementares e suplementares.
Complementares: São os ângulo cuja medida somada ao ângulo dado, resulta em 90 °, ou seja, é "quanto falta para 90°"
Suplementares: São os ângulos cuja medida somada ao ângulo dado, resulta em 180 °, ou seja, é quanto falta para 180°
Assim, vamos chamar nossos ângulos desconhecidos de X e Y
Pelo enunciado:
Complemento de dois ângulos temos
(90° - X) e (90° - Y)
A soma é 130 ° logo:
(90° - X ) + (90° - Y) = 130 °
90° - X + 90° - Y = 130 °
180 ° -X -Y = 130 °
- X - Y = - 50 ° ( multiplicando por -1 ambos lados da igualdade )
X + Y = 50 ° (equação I)
Agora a outra informação: a diferença
entre seus suplementos é 10°
Suplemento de dois ângulos temos:
(180° - X) e (180° - Y)
A diferença é 10°, então
(180° - X) - (180° - Y) = 10°
180° - X - 180° + Y = 10°
-X + Y = 10 ° equação (II)
Agora vamos somar as equações (I) e (II) que nos leva a um sistema de 2 equações com 2 incógnitas:
X + Y = 50° (I)
- X + Y = 10° (II)
(I) + (II): X - X + Y + Y = 60°
2Y = 60°
Y = 60°÷2
Y = 30°
Substituindo-se o valor de Y na equação (I) temos:
X + Y = 50°
X + 30° = 50°
X = 50° - 30°
X = 20°
Logo X = 20° e Y = 30°
10. (IFG) Supondo que a'//a e b'//b, marque a alternativa correta.
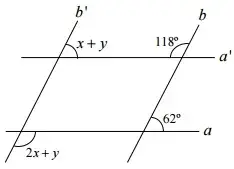
- x = 31° e y = 31°
- x = 56° e y = 6°
- x = 6° e y = 32°
- x = 28° e y = 34°
- x = 34° e y = 28°
Resposta: B
Resolução: 2x + y = 118
x + y = 62
cheguei a essa conclusão pela regra de congruência dos ângulos. Assim, x + y é correspondente ao 62 e o 2x + y é correspondente ao 118. sabendo disso, é só diminuir e teremos que x = 56