Prismas

01. (UFOP–MG) A área total de um cubo cuja diagonal mede 5√3 cm é

1. 140 cm²
2. 150 cm²
3. 120√2 cm²
4. 100√3 cm²
5. 450 cm²

02. (Ufpe) Dois cubos C1 e C2 são tais que a aresta de C1 é igual à diagonal de C2. Se V1 e V2‚ são, respectivamente, os volumes dos cubos de C1 e C2, então, a razão V1/V2‚ é igual a:

1. ³√3
2. √27
3. 1/√27
4. 1/³√3
5. ³√9

03. (FEI–SP) As medidas das arestas de um paralelepípedo retângulo são proporcionais a 2, 3 e 4. Se sua diagonal mede 2√29 cm, seu volume, em centímetros cúbicos, é:

1. 24
2. 24√29
3. 116
4. 164
5. 192

04. (PUC-SP) Na figura a seguir, tem-se o prisma reto ABCDEF, no qual DE = 6 cm, EF = 8 cm e DE é perpendicular a EF.

Se o volume desse prisma é 120 cm3, a sua área total, em centímetros quadrados, é:

1. 144
2. 156
3. 160
4. 168
5. 172

05. (FGV–SP) Em uma piscina retangular com 10 m de comprimento e 5 m de largura, para elevar o nível de água em 10 cm são necessários:

1. 500 l de água
2. 5 000 l de água
3. 10 000 l de água
4. 1 000 l de água
5. 50 000 l de água

06. (PUC-SP) Um tanque de uso industrial tem a aforma de um prisma cuja base é um trapézio isósceles. Na figura a seguir, são dadas as dimensões, em metros, do prisma:

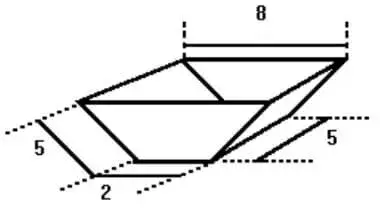
O volume desse tanque, em metros cúbicos, é:

1. 50
2. 60
3. 80
4. 100
5. 120

07. (UECE) Com 42 cubos de 1 cm de aresta formamos um paralelepípedo cujo perímetro da base é 18 cm. A altura deste paralelepípedo, em cm, é:

1. 4
2. 3
3. 2
4. 1

08. (Fuvest) Dois blocos de alumínio, em forma de cubo, com arestas medindo 10cm e 6cm são levados juntos à fusão e em seguida o alumínio líquido é moldado como um paralelepípedo reto de arestas 8cm, 8cm e xcm. O valor de x é:

1. 16
2. 17
3. 18
4. 19
5. 20

09. (Cefet-MG) De uma piscina retangular com 12 metros de comprimento por 6 metros de largura, foram retirados 10 800 litros de água. É correto afirmar que o nível de água baixou:

1. 15 cm
2. 16 cm
3. 16,5 cm
4. 17 cm
5. 18,5 cm

10. (Unesp) Uma piscina retangular de 10,0m x 15,0m e fundo horizontal está com água até a altura de 1,5m. Um produto químico em pó deve ser misturado à água à razão de um pacote para cada 4500 litros. O número de pacotes a serem usados é

1. 45
2. 50
3. 55
4. 60
5. 75

11. (FGV-RJ) Uma piscina tem o formato de um paralelepípedo retângulo com as dimensões: 10m de comprimento, 4m de largura e 1,5m de altura.

Inicialmente, a piscina está vazia e é preenchida com água que jorra de um tubo a uma vazão de 250 litros por minuto.

Depois de duas horas e meia, qual a porcentagem do volume de água em relação ao volume total da piscina?

1. 60%
2. 55%
3. 57,5%
4. 52,5%
5. 62,5%

12. (UFPR) Diana pretende distribuir 6 litros de geleia em 25 potes iguais. Cada pote possui internamente o formato de um paralelepípedo de base quadrada com 5 cm de lado. Dividindo igualmente a geleia em todos os potes, qual é a altura interna que a geleia atingirá em cada recipiente?

1. 6,0 cm.
2. 7,5 cm.
3. 9,6 cm.
4. 15,0 cm.
5. 24,0 cm.

13. (UFT) Uma empresa de logística trabalha com caixas de papelão padronizadas. Um dos modelos de caixa de papelão, denominado TIPO 1, tem dimensões 50cmx60cmx83cm conforme imagem a seguir:

Esta empresa utiliza um único modelo de palete com dimensões 1,20mx1,00m, conforme ilustração seguinte:

Por questões operacionais e de logística, a empresa definiu que cada palete deve ser carregado com no máximo três metros cúbicos (3m³) de volume. Além disso, as caixas não podem ser empilhadas sobre o palete, de forma a ultrapassarem as dimensões de sua base.

Com base nessas informações e levando em consideração que as caixas de papelão estejam com seu volume máximo, é CORRETO afirmar que o número máximo de caixas do TIPO 1 que podem ser carregadas em um palete é:

1. 4
2. 10
3. 12
4. 16

14. (PUC-PR) Considere um prisma reto cuja base é o triângulo ABC retângulo em A, sendo a medida do lado AB, 6 cm e a projeção ortogonal do lado AB sobre a hipotenusa BC é 3,6 cm. A altura do prisma é 5 cm.

O volume em cm³ deste prisma é

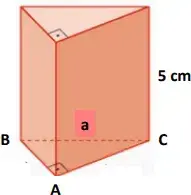
1. 36.
2. 100.
3. 120.
4. 150.
5. 240.

15. (FGV-SP) Uma piscina tem o formato de um paralelepípedo retângulo com as dimensões: 10m de comprimento, 4m de largura e 1,5m de altura.

Inicialmente, a piscina está vazia e é preenchida com água que jorra de um tubo a uma vazão de 250 litros por minuto.

Depois de duas horas e meia, qual a porcentagem do volume de água em relação ao volume total da piscina?

1. 60%
2. 55%
3. 57,5%
4. 52,5%
5. 62,5%

16. (FAMEMA) Um recipiente transparente possui o formato de um prisma reto de altura 15 cm e base quadrada, cujo lado mede 6 cm. Esse recipiente está sobre uma mesa com tampo horizontal e contém água até a altura de 10 cm, conforme a figura.

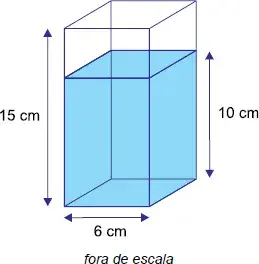
Se o recipiente for virado e apoiado na mesa sobre uma de suas faces não quadradas, a altura da água dentro dele passará a ser de

1. 4 cm.
2. 3,5 cm.
3. 3 cm.
4. 2,5 cm.
5. 2 cm.

17. (UECE) Em um prisma triangular reto, a base XYZ é um triângulo retângulo cuja medida dos catetos são respectivamente 3 m e 4 m.

Se a medida do volume desse prisma é 18 m³, então, a medida, em metros quadrados, da superfície total desse prisma é

1. 36.
2. 48.
3. 32.
4. 52.

18. (UFRGS) Um prisma reto de base hexagonal regular tem a mesma altura de um prisma cuja base é um triângulo equilátero. Considere h a medida da aresta da base do prisma hexagonal e t a medida da aresta da base do prisma triangular. Se ambos os prismas têm o mesmo volume, então a razão $\frac{h}{t}$ vale

1. $\frac{1}{\mathrm{\surd 6}}$
2. $\frac{1}{6}$
3. 1.
4. √6
5. 6

19. (UEA) Um ourives fundiu dois blocos de ouro, ambos de formato cúbico, de arestas medindo 10 mm e 6 mm. Em seguida, usou todo o ouro líquido resultante da fusão para compor um novo bloco com a forma de um prisma reto de base quadrada, de área da base igual a 64 mm² e altura igual a x mm. Admitindo-se que na fusão não ocorreu perda de material, o valor de x é igual a

1. 18,0.
2. 17,6.
3. 19,0.
4. 14,0.
5. 15,5.

20. (UPE) Qual é a capacidade, em litros, de uma cisterna que tem a forma da figura abaixo?

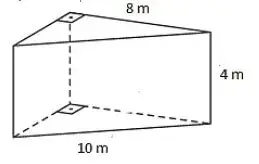
1. 3,2×10⁴
2. 5,2×10³
3. 6,4×10³
4. 9,6×10⁴
5. 10,5×10⁴