Poliedros

01. (Fuvest) O número de faces triangulares de uma pirâmide é 11. Pode-se, então, afirmar que esta pirâmide possui:

1. 33 vértices e 22 arestas.
2. 12 vértices e 11 arestas.
3. 22 vértices e 11 arestas.
4. 11 vértices e 22 arestas.
5. 12 vértices e 22 arestas.

02. (PUCAMP) Sobre as sentenças:

I. Um octaedro regular tem 8 faces quadradas.

II. Um dodecaedro regular tem 12 faces pentagonais.

III. Um icosaedro regular tem 20 faces triangulares.

É correto afirmar que apenas:

1. I é verdadeira.
2. II é verdadeira.
3. III é verdadeira.
4. I e III são verdadeiras.
5. II e III são verdadeiras.

03. (Cesgranrio) Um poliedro convexo é formado por 4 faces triangulares, 2 faces quadrangulares e 1 face hexagonal. O número de vértices desse poliedro é de:

1. 6
2. 7
3. 8
4. 9
5. 10

04. (UFRS) Um poliedro convexo tem seis faces triangulares e cinco faces quadrangulares. O número de arestas e de vértices do poliedro é, respectivamente:

1. 34 e 10
2. 19 e 10
3. 34 e 20
4. 12 e 10
5. 19 e 12

05. (Cesgranrio) Um poliedro convexo tem 14 vértices. Em 6 desses vértices concorrem 4 arestas, em 4 desses vértices concorrem 3 arestas e, nos demais vértices, concorrem 5 arestas. O número de faces desse poliedro é igual a:

1. 16
2. 18
3. 24
4. 30
5. 44

06. (UFPI) Em um poliedro convexo, o número de arestas excede o número de faces em 18. O número de vértices desse poliedro é:

1. 10
2. 20
3. 24
4. 30
5. 32

07. (PUC-PR) Quantas arestas tem um poliedro convexo de faces triangulares em que o número de vértices é 3/5 do número de faces?

1. 60
2. 30
3. 25
4. 20
5. 15

08. (UEL) Para explicar a natureza do mundo, Platão “[...] apresenta a teoria segundo a qual os ‘quatro elementos’ admitidos como constituintes do mundo - o fogo, o ar, a água e a terra - [...] devem ter a forma de sólidos regulares. [...] Para não deixar de fora um sólido regular, atribuiu ao dodecaedro a representação da forma de todo o universo.” (DEVLIN, Keith. Matemática: a ciência dos padrões. Porto: Porto Editora, 2002. p.119.)

As figuras a seguir representam esses sólidos geométricos, que são chamados de poliedros regulares. Um poliedro é um sólido limitado por polígonos. Cada poliedro tem um certo número de polígonos em torno de cada vértice. Uma das figuras anteriores representa um octaedro. A soma das medidas dos ângulos em torno de cada vértice desse octaedro é:

1. 180°
2. 240°
3. 270°
4. 300°
5. 324°

09. (Cesgranrio) Um poliedro convexo é formado por 80 faces triangulares e 12 pentagonais. O número de vértices do poliedro é:

1. 80
2. 60
3. 50
4. 48

10. (Mack) Considere uma pirâmide cuja base é um polígono convexo. Se a soma das medidas dos ângulos internos de todas as suas faces é 3600º, o número de lados da base dessa pirâmide é igual a:

1. 11
2. 12
3. 9
4. 10
5. 8

11. (EEAR) Sabendo que o dodecaedro regular possui 20 vértices, o número de arestas desse poliedro é

1. 16
2. 28
3. 30
4. 32

12. (USS) O poliedro desenhado a seguir, cuja aresta mede 10 cm, é formado por nove faces, sendo quatro triângulos equiláteros e cinco quadrados.

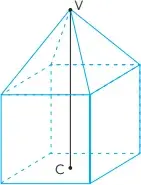
Os pontos V e C, são respectivamente, o vértice do poliedro e o centro da face quadrada oposta. A distância, em cm, entre os pontos V e C é igual a:

1. 15
2. 20
3. 20√2
4. 10+5√2

13. (UECE) Um poliedro convexo com 32 vértices possui apenas faces triangulares. O número de arestas deste poliedro é

1. 100.
2. 120.
3. 90.
4. 80.

14. (UERJ) Dois dados, com doze faces pentagonais cada um, têm a forma de dodecaedros regulares. Se os dodecaedros estão justapostos por uma de suas faces, que coincidem perfeitamente, formam um poliedro côncavo, conforme ilustra a figura.

Considere o número de vértices V, de faces F e de arestas A desse poliedro côncavo.

A soma V + F + A é igual a:

1. 102
2. 106
3. 110
4. 112

15. (UEFS)

Um tipo de bola de futebol é inspirado no icosaedro truncado, que é um poliedro convexo formado por 12 faces pentagonais e 20 faces hexagonais.

O número de vértices desse poliedro é

1. 40
2. 48
3. 60
4. 64
5. 76

16. (FATEC) Em um jogo de tabuleiro, para cada jogada são lançados dois dados, um branco e outro vermelho. Os dados são honestos, têm a forma de tetraedro regular e com um único número em cada face.

O dado branco tem as faces numeradas por: –1, 0, 1 e 2.

O dado vermelho tem as faces numeradas por: –2, –1, 0 e 1.

O jogador lança os dados e observa a face em que cada um deles se apoia, isto é, a que está voltada para baixo.

Pelas regras do jogo, o jogador avança ou retrocede, no tabuleiro, quando o produto dos números obtidos nos dados for positivo ou negativo, respectivamente.

Em uma jogada, o número de modos distintos em que os resultados dos dados levam a um retrocesso é

1. 4.
2. 5.
3. 6.
4. 7.
5. 8.

17. (IFAL) O número de vértices de um poliedro convexo com 3 faces triangulares, 5 faces pentagonais e 2 faces hexagonais é

1. 11
2. 12
3. 13
4. 14
5. 15

18. (ACAFE) Qual o volume de um octaedro regular cuja soma das medidas das arestas é 144 cm?

1. 576(2)^0,5cm³
2. 642 cm³
3. 324(3)^0,5cm³
4. 400 cm³

19. (UECE) Se um poliedro convexo tem exatamente 20 faces e todas são triangulares, então o número de vértices deste poliedro é

1. 16.
2. 14.
3. 12.
4. 10.

20. (UCPEL) Um poliedro convexo possui 9 faces, 5 quadrangulares e 4 triangulares. Então, o número de arestas e o de vértices desse poliedro, respectivamente, é

1. 16 e 9
2. 18 e 6
3. 12 e 10
4. 14 e 8
5. 10 e 6