Paralelepípedo

01. (UFPA) Qual a área total de um paralelepípedo reto cujas dimensões são 2,3 e 4 cm?

1. 24 cm²
2. 26cm²
3. 30 cm³
4. 40 cm²
5. 52cm²

02. (PUC-PR Inverno) Tati está testando um novo material ecológico para a fabricação de calçada anti-insetos.

Se um paralelepípedo desse novo material tem a massa de 10 kg, é CORRETO afirmar que um outro paralelepípedo semelhante feito do mesmo material:

1. Mas duas vezes menor tem a massa de 2,5kg.
2. Mas duas vezes maior tem a massa de 20kg.
3. De massa 20kg é quatro vezes maior.
4. De massa 20kg é cinco vezes maior.
5. Mas duas vezes menor tem a massa de 1,25kg.

03. (UEPG-PR) As medidas Internas de uma caIxa-d'água em forma de paralelepípedo retângulo são: 1,2 m, 1 m e 0,7 m. Sua capacidade é de:

1. 8 400 litros
2. 84 litros
3. 840 litros
4. 8,4 litros
5. n.d.a.

04. (FGV-RJ) Uma piscina tem o formato de um paralelepípedo retângulo com as dimensões: 10m de comprimento, 4m de largura e 1,5m de altura.

Inicialmente, a piscina está vazia e é preenchida com água que jorra de um tubo a uma vazão de 250 litros por minuto.

Depois de duas horas e meia, qual a porcentagem do volume de água em relação ao volume total da piscina?

1. 60%
2. 55%
3. 57,5%
4. 52,5%
5. 62,5%

05. (FGV-SP) Sobre a face quadrada BCHG do paralelepípedo reto-retângulo ABCDEFGH foram traçados GQ e HP, intersectando-se em J, com P e Q dividindo BC em três segmentos congruentes tais que BP = PQ = QC. Sabe-se ainda que HE = 8 cm e que GJHEFI é um prisma reto de volume 81 cm3.

O volume do paralelepípedo ABCDEFGH, em cm³, é igual a

1. 243.
2. 216.
3. 192.
4. 96.
5. 72.

06. (FATEC) De um paralelepípedo retorretângulo de 30 cm, 4 cm e 15 cm, é removido um semicilindro circular reto de altura 4 cm e base de diâmetro 20 cm, obtendo-se uma peça como mostra a figura.

Assim sendo, o volume da peça é, em centímetros cúbicos, Adote π = 3.

1. 1 100.
2. 1 200.
3. 1 300.
4. 1 400.
5. 1 500.

07. (ITA) Considere a classificação: dois vértices de um paralelepípedo são não adjacentes quando não pertencem à mesma aresta. Um tetraedro é formado por vértices não adjacentes de um paralelepípedo de arestas 3 cm, 4 cm e 5 cm. Se o tetraedro tem suas arestas opostas de mesmo comprimento, então o volume do tetraedro é, em cm3 :

1. 10
2. 12
3. 15
4. 20
5. 30

08. (UFPR) Diana pretende distribuir 6 litros de geleia em 25 potes iguais. Cada pote possui internamente o formato de um paralelepípedo de base quadrada com 5 cm de lado. Dividindo igualmente a geleia em todos os potes, qual é a altura interna que a geleia atingirá em cada recipiente?

1. 6,0 cm.
2. 7,5 cm.
3. 9,6 cm.
4. 15,0 cm.
5. 24,0 cm.

09. (UNIVESP) O nível da água contida em um reservatório na forma de um paralelepípedo reto retângulo, de 4 m de comprimento e 3 m de largura, atingia a altura de 1,5 m. Sabe-se que houve um consumo de 6 m3 de água desse reservatório, sem haver reposição, e a altura do nível da água restante no reservatório passou a ser indicada por h, conforme mostra a figura.

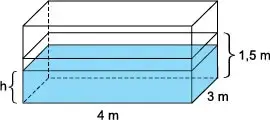
Nessas condições, é correto afirmar que a medida indicada por h na figura é igual a

1. 1,25 m.
2. 1 m.
3. 0,8 m.
4. 0,75 m.
5. 0,5 m.

10. (CESGRANRIO) Observe, na imagem, a planificação de uma caixa com formato de paralelepípedo reto-retângulo.

Considerando-se as medidas apresentadas, qual é, em cm², a área da menor face dessa caixa?

1. 96
2. 120
3. 160
4. 192
5. 192

11. (FGV-SP) Uma piscina tem o formato de um paralelepípedo retângulo com as dimensões: 10m de comprimento, 4m de largura e 1,5m de altura.

Inicialmente, a piscina está vazia e é preenchida com água que jorra de um tubo a uma vazão de 250 litros por minuto.

Depois de duas horas e meia, qual a porcentagem do volume de água em relação ao volume total da piscina?

1. 60%
2. 55%
3. 57,5%
4. 52,5%
5. 62,5%

12. (FMC) Uma caixa d’água, em forma de um paralelepípedo retângulo, tem dimensões iguais a 110 cm, 90 cm e 100 cm. Sua capacidade, em litros, é numericamente igual a

1. 99 000.
2. 9 900.
3. 990.
4. 900.
5. 99.

13. (URCA) As dimensões de um paralelepípedo retângulo são dadas por α cm, b cm e 3α cm.

Sabendo que o volume desse paralelepípedo é 240 cm³ e sua área total é 256 cm², determine em cm o valor de α.

1. 6
2. 5
3. 4
4. 8
5. 9

14. (UEA) De acordo com o projeto original, um reservatório, com formato de paralelepípedo reto retângulo, de volume V, teria 4 m de comprimento, 2,5 m de largura e 2 m de altura, conforme figura.

Pretende-se modificar esse projeto, mantendo-se a forma do reservatório, o volume V e a altura igual a 2 m.

Nessas condições, se a medida da largura for reduzida em 20%, a medida do comprimento deverá ser

1. 4,75 m.
2. 4,5 m.
3. 4,25 m.
4. 4,8 m.
5. 5,0 m.

15. (UFPR) A piscina usada nas competições de natação das Olimpíadas Rio 2016 possui as medidas oficiais recomendadas: 50 metros de extensão, 25 metros de largura e 3 metros de profundidade. Supondo que essa piscina tenha o formato de um paralelepípedo retângulo, qual dos valores abaixo mais se aproxima da capacidade máxima de água que essa piscina pode conter?

1. 37.500 litros.
2. 375.000 litros.
3. 3.750.000 litros.
4. 37.500.000 litros.
5. 375.000.000 litros.

16. (UEA - SIS) Em um paralelepípedo reto-retângulo, a face ABCD é oposta a face EFGH, conforme ilustra a figura.

Sendo J o ponto de encontro entre as retas EG e FH, a reta DJ é

1. paralela ao plano ABF.
2. pertencente ao plano CGH.
3. paralela à reta EF.
4. reversa à reta BH.
5. concorrente com a reta BF.

17. (UNICAMP) Um paralelepípedo retângulo tem faces de áreas 2 cm², 3 cm² e 4 cm². O volume desse paralelepípedo é igual a

1. 2√3 cm³.
2. 2√6 cm³.
3. 24 cm³.
4. 12 cm³.

18. (UEFS) Um cubo de aresta igual a 6 cm foi totalmente perfurado entre duas faces opostas. A forma do furo é a de um paralelepípedo reto-retângulo de bases quadradas de lado igual a 2 cm, como mostra a figura.

Se o custo para pintar totalmente esse cubo perfurado com uma tinta especial é de R$ 0,05 por cm², então o valor total gasto nessa pintura será igual a

1. R$ 10,60.
2. R$ 12,80.
3. R$ 12,20
4. R$ 10,40.
5. R$ 13,20.

19. (UNIFENAS) Considere que uma piscina tenha o formato de um paralelepípedo, cujas dimensões sejam: 10 metros de comprimento, 5 metros de largura e 2 metros de profundidade. Caso utilize o revestimento cerâmico de 20 cm por 20 cm, quantas peças utilizará para recobrir o fundo acrescido das laterais?

1. 400.
2. 900.
3. 1900.
4. 2750.
5. 2760.

20. (PUC-RS) Muitos prédios que estão sendo construídos em nossa cidade possuem caixas d’água com a forma de um paralelepípedo. Um construtor quer adquirir duas delas que tenham internamente a mesma altura, mas diferindo na base, que deverá ser quadrada em ambas. A primeira deverá ter capacidade para 16000 litros, e a segunda para 25000 litros. A razão entre a medida do lado da base da primeira e a da segunda, em decímetros, é

1. 0,08
2. 0,60
3. 0,75
4. 0,80
5. 1,25