Cones

01. (Fuvest) Deseja-se construir um cone circular reto com 4cm de raio da base e 3cm de altura. Para isso, recorta-se, em cartolina, um setor circular para a superfície lateral e um círculo para a base. A medida do ângulo central do setor circular é:

1. 144°
2. 192°
3. 240°
4. 288°
5. 336°

02. (Cefet-SC) Dado um copo em forma de cilindro e outro de forma cônica de mesma base e altura. Se eu encher completamente o copo cônico com água e derramar toda essa água no copo cilíndrico, quantas vezes terei que fazê-lo para encher completamente esse copo?

1. Apenas uma vez.
2. Duas vezes.
3. Três vezes.
4. Uma vez e meia.
5. É impossível saber, pois não se sabe o volume de cada sólido.

03. (UNIFOR-CE) Em um cone reto, a área da base é 9π cm² e a geratriz mede 3√10 cm. O volume desse cone, em centímetros cúbicos, é:

1. 27π
2. 36π
3. 48π
4. 54π
5. 81π

04. (Cesgranrio) Um copo de papel, em forma de cone, é formado enrolando-se um semicírculo que tem um raio de 12cm. O volume do copo é de, aproximadamente:

1. 390 cm²
2. 350 cm²
3. 300 cm²
4. 260 cm²
5. 230 cm²

Começa em 4:22

05. (UEMA) O volume de um cone equilátero que tem como área da base Ab = 12π m² é:

1. 72π m³
2. 24π m³
3. 36π m³
4. 28π m³
5. 40π m³

06. (PUC-MG) Um monte de areia tem a forma de um cone circular reto, com volume V= 4πm³. Se o raio da base é igual a dois terços da altura desse cone, pode-se afirmar que a medida da altura do monte de areia, em metros, é:

1. 2
2. 3
3. 4
4. 5

07. (UFPI) Se 8π cm² é a área lateral de um cone circular reto cujo raio da base é 2 cm, então a altura desse cone, em cm, é:

1. √2
2. √3
3. √6
4. 2√2
5. 2√3

08. (Cefet-PR) O raio da base de um cone circular reto mede 3 m e o perímetro de sua seção meridiana mede 16 m. O volume desse cone mede:

1. 8π m³
2. 10π m³
3. 14π m³
4. 12π m³
5. 36π m³

09. (MACK-SP) A planificação da superfície lateral de um cone é um semicírculo de raio 10√3. O volume do cone é:

1. 357π
2. 573π
3. 375π
4. 537π
5. 735π

10. (UFGO) A terra retirada na escavação de uma piscina semicircular de 6 m de raio e 1,25 m de profundidade foi amontoada, na forma de um cone circular reto, sobre uma superfície horizontal plana.

Admita que a geratriz do cone faça um angulo de 60° com a vertical e que a terra retirada tenha volume de 20% maior do que o volume da piscina. Nessas condições, a altura do cone, em metros, é de:

1. 2,0
2. 2,8
3. 3,0
4. 3,8
5. 4,0

11. (UERJ) A figura a seguir representa a trajetória curva do ponto P sobre a superfície lateral de um cone circular reto cujo raio da base mede 10 cm e a geratriz, 60 cm. O ponto P inicia sua trajetória no ponto A, que pertence à circunferência da base, e dá uma volta completa em torno do cone, até retornar ao ponto A.

Com a planificação da superfície lateral do cone, é possível calcular o menor comprimento da trajetória percorrida por P, que corresponde, em centímetros, a:

1. 50
2. 60
3. 18π
4. 20π

12. (ITA) A superfície lateral de um cone circular reto corresponde a um setor circular de 216°, quando planificada. Se a geratriz do cone mede 10 cm, então a medida de sua altura, em cm, é igual a

1. 5.
2. 6.
3. 7.
4. 8.
5. 9.

13. (Mackenzie) Se um cone reto tem altura igual a 12 cm e seu volume é 64π cm³, então sua geratriz, em cm, mede

1. 20
2. 10√2
3. 4√10
4. 4√2
5. 25√10

Resolução: Temos um cone reto que possui altura h=12 cm e volume de 64π e temos que achar o valor da geratriz que é qualquer segmento que tenha uma extremidade no vértice do cone e a outra na curva que envolve a base.

Portanto, temos que ao desenhar o cone, A é o vértice do cone, B é o centro da base do cone e C é a geratriz, formando um triângulo. A distância entre B e C é o raio da base do cone.

Como o volume do cone é dado por:

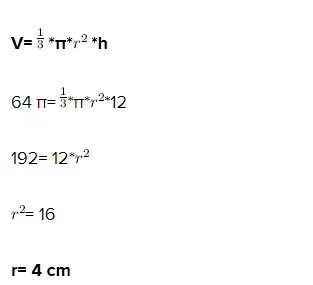
Como o raio é igual ao segmento BC, e AB corresponde à altura também conhecida, calculamos então AC que é a geratriz do cone (hipotenusa do triângulo):

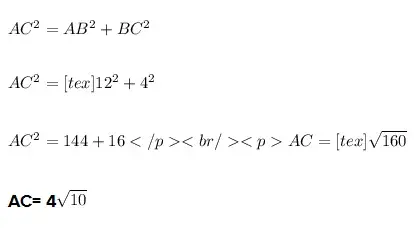
14. (UFN) Para armazenar a água das chuvas foi construída uma cisterna no formato de um cone circular reto de altura h (metros), com vértice para baixo e com eixo vertical. A capacidade total da cisterna é de 13 500 litros.

Quando o nível está em h/3, qual o volume de água disponível na cisterna?

1. 500 litros.
2. 1 500 litros.
3. 2 250 litros.
4. 4 500 litros.
5. 6 750 litros.

15. (UFAM PSC) Um copo de sorvete é um cone de 10cm de altura e 4cm de diâmetro na base. Um sorveteiro coloca no copo duas bolas de sorvete com formato esférico e que possui diâmetro de 4cm. Se o sorvete derreter dentro do cone, então:

1. haverá transbordamento de 8cm³ de sorvete.
2. não haverá transbordamento e ainda sobrará espaço no copo para 8cm³ de sorvete.
3. não haverá transbordamento, pois os dois sólidos possuem o mesmo volume.
4. haverá transbordamento de 10cm³ de sorvete.
5. não haverá transbordamento e ainda sobrará espaço no copo para 10cm³ de sorvete.

16. (ESA) A geratriz de um cone circular reto de altura 8 cm é 10 cm, então a área da base desse cone é:

1. 64 π cm²
2. 9 π cm²
3. 16 π cm²
4. 36 π cm²
5. 25 π cm²

17. (UNESP) Um cone circular reto, de vértice V e raio da base igual a 6 cm, encontra-se apoiado em uma superfície plana e horizontal sobre uma geratriz. O cone gira sob seu eixo de revolução que passa por V, deslocando-se sobre a superfície plana horizontal, sem escorregar, conforme mostra a figura.

O cone retorna à posição inicial após o círculo da sua base ter efetuado duas voltas completas de giro. Considerando que o volume de um cone é calculado pela fórmula πr²h, o volume do cone da figura, em cm³, é igual a

1. 72√3π
2. 48√3π
3. 36√3π
4. 18√3π
5. 12√3π

18. (UPE) Um cone reto está inscrito num cubo de aresta 8 cm. Se a altura do cone e o diâmetro de sua base têm medidas iguais, qual é a diferença entre as medidas dos seus volumes? Considere π = 3,0

1. 128 cm³
2. 256 cm³
3. 384 cm³
4. 424 cm³
5. 512 cm³

19. (UDESC) A base de um cone reto está inscrita em uma face de um cubo e seu vértice está no centro da face oposta. Se o volume do cone é 2π/3 metros cúbicos, a área do cubo (em metros quadrados) é igual a:

1. 8
2. 24
3. 16
4. 20
5. 4

20. (Mackenzie) Fazendo-se a planificação de um cone de altura 15 cm, observa-se que sua superfície lateral é um setor circular, cujo ângulo central mede 4π/3 radianos.

Então, o volume do cone, em cm3, é

1. 500π
2. 900π
3. 1500π
4. 2025π
5. 2700π