Cilindros

01. (Fuvest) A uma caixa d'água de forma cúbica com 1 metro de lado, está acoplado um cano cilíndrico com 4cm de diâmetro e 50m de comprimento. Num certo instante, a caixa está cheia de água e o cano vazio.

Solta-se a água pelo cano até que fique cheio. Qual o valor aproximado da altura da água na caixa no instante em que o cano ficou cheio?

1. 90 cm.
2. 92 cm.
3. 94 cm.
4. 96 cm.
5. 98 cm.

02. (Enem) Uma artesã confecciona dois diferentes tipos de vela ornamental a partir de moldes feitos com cartões de papel retangulares de 20 m x 10 cm (conforme ilustram as figuras abaixo). Unindo dois lados opostos do cartão, de duas maneiras, a artesã forma cilindros e, em seguida, os preenche completamente com parafina.

Supondo que o custo da vela seja diretamente proporcional ao volume da parafina empregado, o custo da vela do tipo I, em relação ao custo da vela do tipo II, será:

1. o triplo.
2. o dobro.
3. igual.
4. a metade.
5. a terça parte.

03. (UFPR) As duas latas na figura abaixo possuem internamente o formato de cilindros circulares retos, com as alturas e diâmetros da base indicados. Sabendo que ambas as latas têm o mesmo volume, qual o valor aproximado da altura h?

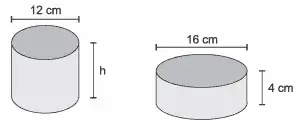
1. 5 cm
2. 6 cm
3. 6,25 cm
4. 7,11 cm
5. 8,43 cm

04. (IFAL) Arquimedes, para achar o volume de um objeto de forma irregular, mergulhou-o num tanque cilíndrico circular reto contendo água. O nível da água subiu 10 cm sem transbordar. Se o diâmetro do tanque é 20 cm, qual o volume do objeto? Use π = 3.

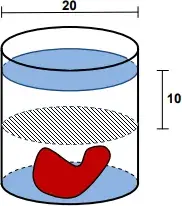
1. 1000π
2. 2000π
3. 3000π
4. 4000π
5. 5000π

05. (Puccamp) Numa indústria, deseja-se utilizar tambores cilíndricos para a armazenagem de certo tipo de óleo. As dimensões dos tambores serão 30cm para o raio da base e 80cm para a altura. O material utilizado na tampa e na lateral custa R$100,00 o metro quadrado. Devido à necessidade de um material mais resistente no fundo, o preço do material para a base inferior é de R$200,00 o metro quadrado.

Qual o custo de material para a confecção de um desses tambores sem contar as perdas de material?

(Em seus cálculos, considere π=3,14.)

1. R$ 235,50
2. R$ 242,50
3. R$ 247,90
4. R$ 249,10
5. R$ 250,00

06. (Cesgranrio) Um recipiente com a forma de um cilindro reto, cujo diâmetro da base mede 40 cm e altura 100/π cm, armazena um certo líquido, que ocupa 40% de sua capacidade. O volume do líquido contido nesse recipiente é, em litros, aproximadamente, igual a:

1. 16
2. 18
3. 20
4. 30
5. 40

07. (Faap) Sabendo-se que uma lata de azeite cilíndrica tem 8cm de diâmetro e 18,5cm de altura e ainda que nela vem marcado o conteúdo 900ml, o volume de ar contido na lata “cheia” e “fechada” é: (Adote π = 3,14)

1. 29,44 ml
2. 10,0 ml
3. 15,60 ml
4. 21,72 ml
5. 35,50 ml

08. (UFF) A figura abaixo representa o paralelogramo MNPQ.

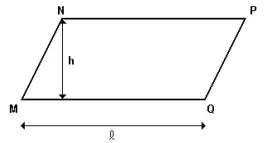
O volume do sólido obtido pela rotação do paralelogramo em torno da reta suporte do lado MQ é dado por:

1. π h² (l+h) / 2
2. π h² l/2
3. π h² (l+h)
4. π h (l+h)²
5. π h² l

09. (Faap) Sabendo-se que uma lata de azeite cilíndrica tem 8cm de diâmetro e 18,5cm de altura e ainda que nela vem marcado o conteúdo 900ml, o volume de ar contido na lata "cheia" e "fechada" é: (Adote π = 3,14)

1. 29,44 ml
2. 10,0 ml
3. 15,60 ml
4. 21,72 ml
5. 35,50 ml

10. (Ufpe) Qual das propostas a seguir pode ser utilizada para duplicar o volume de um cilindro modificando seu raio da base e sua altura?

1. Duplicar o raio e manter a altura.
2. Aumentar a altura em 50% e manter o raio.
3. Aumentar o raio em 50% e manter a altura.
4. Duplicar o raio e reduzir a altura à metade.
5. Duplicar a altura e reduzir o raio à metade.

11. (EEAR) Um cilindro circular reto, de altura igual a 2/3 do raio da base e de 12 cm² de área lateral, possui raio da base igual a _____ cm.

1. 5
2. 4
3. 3
4. 2

12. (ETEC) Uma questão ambiental relevante, na atualidade, remete ao acúmulo e ao descarte de resíduos sólidos. A indústria nuclear é responsável pelo armazenamento e controle dos rejeitos que produz.

Suponha que uma indústria nuclear armazene seus resíduos em recipientes cilíndricos, cuja altura é igual a 4 m e o diâmetro da base igual a 12 m. Contudo, devido a mudanças operacionais, decide-se alterar a altura e o raio destes recipientes cilíndricos de tal maneira que o novo recipiente:

• tenha volume igual a 62,5% do volume do recipiente anterior;

• e possua raio da base igual à metade do raio da base do recipiente anterior;

Desta forma, a altura do novo recipiente cilíndrico deve ser, em metros, igual a

• Lembre que: V = 𝜋r² · h em que,

• V é o volume do cilindro;

• r é o raio do círculo da base;

• h é a altura do cilindro.

1. 8.
2. 10.
3. 16.
4. 20.
5. 40.

13. (FGV-SP) Um cilindro circular reto de altura igual ao diâmetro da base está inscrito em um cone circular reto. O cone tem diâmetro 10, altura 12 e seu eixo de revolução coincide com o do cilindro.

O diâmetro da base do cilindro é igual a

1. 16/3
2. 60/11
3. 6.
4. 25/4.
5. 7.

14. (FAMEMA) A área lateral de um cilindro circular reto é 72π cm² e seu volume é 6 vezes o volume de um cone circular reto que tem 18 cm de altura.

Sabendo que a medida do raio da base do cilindro é o dobro da medida do raio da base do cone, então a medida do raio da base do cone é

1. 2 cm.
2. 6 cm.
3. 4 cm.
4. 8 cm.
5. 10 cm

15. (PUC-PR) Um medicamento que dilata os vasos e artérias do corpo humano é ministrado e aumenta o diâmetro em 20% de determinada artéria.

Considerando que a artéria se assemelha a um cilindro circular reto, o fluxo sanguíneo nessa artéria aumenta em

1. 10%
2. 20%
3. 21%
4. 40%
5. 44%

16. (IFRN) Para fabricar barras de aço que serão usadas nas grades de um presídio, uma empresa derreteu uma bola maciça de aço de raio 2m. As barras que serão fabricadas terão formato cilíndrico, com raio da base medindo 5cm e altura de 2m. Considerando 𝝅=3, a quantidade máxima de barras que poderão ser fabricadas com o aço obtido pelo derretimento da bola, aproximadamente, é

1. 123.
2. 213.
3. 1.233.
4. 2.133.

17. (UESB) Um laboratório pretende embalar latas cilíndricas de mesmas dimensões, contendo medicamento líquido, em caixas retangulares, medindo 104cm x 72cm, de modo que seja aproveitado, ao máximo, o espaço disponível e que, o diâmetro da base das latas seja o maior possível.

Nessas condições, pode-se afirmar que o raio da base das latas deverá ser igual a

1. 10cm.
2. 9cm.
3. 8cm.
4. 5cm.
5. 4cm.

18. (UECE) A medida, em m², da área da superfície total (área lateral e bases) de um cilindro circular reto tal que a medida da altura e a medida do raio da base são ambas iguais a 2 m é

1. 14 π
2. 12 π
3. 16 π
4. 10 π

19. (UEG) Deseja-se construir um reservatório cilíndrico circular reto com 8 metros de diâmetro e teto no formato de hemisfério. Sabendo-se que a empresa responsável por construir o teto cobra R$ 300,00 por m², o valor para construir esse teto esférico será de

use π = 3,1

1. R$ 22.150,00
2. R$ 32.190,00
3. R$ 38.600,00
4. R$ 40.100,00
5. R$ 29.760,00

20. (UECE) Considere um mês em que o total de chuva registrada em Fortaleza seja de 300 mm. Suponha que a distribuição de chuva seja homogênea em toda a área do município. Considere um tanque cilíndrico sem tampa, que recebe água coletada diretamente pela exposição a essa chuva durante esse mês. A área da base do tanque é de 10 m². No mês em questão, o volume coletado no recipiente é, em litros,

1. 300.
2. 3.000.
3. 30.
4. 30.000.