Multiplos e Divisores

01. (UFPR) Em uma determinada manhã, um médico atendeu 6 pacientes. A duração do atendimento referente a cada paciente é apresentada na tabela ao lado. Com base nas informações fornecidas, conclui-se que o tempo total de atendimento prestado pelo médico naquela manhã foi de:

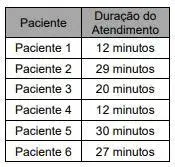
1. 2 horas e 30 minutos.
2. 2 horas e 10 minutos.
3. 1 hora e 50 minutos.
4. 1 hora e 30 minutos.
5. 1 hora e 10 minutos.

02. (UERJ) Uma gerente de loja e seu assistente viajam com frequência para São Paulo e voltam no mesmo dia. A gerente viaja a cada 24 dias e o assistente, a cada 16 dias, regularmente. Em um final de semana, eles viajaram juntos. Depois de x viagens da gerente e y viagens do assistente sozinhos, eles viajaram juntos novamente.

O menor valor de x + y é:

1. 1
2. 2
3. 3
4. 4

03. (UFPR) Rafaela e Henrique participaram de uma atividade voluntária que consistiu na pintura da fachada de uma instituição de caridade. No final do dia, restaram duas latas de tinta idênticas (de mesmo tamanho e cor). Uma dessas latas estava cheia de tinta até a metade de sua capacidade e a outra estava cheia de tinta até 3/4 de sua capacidade. Ambos decidiram juntar esse excedente e dividir em duas partes iguais, a serem armazenadas nessas mesmas latas. A fração que representa o volume de tinta em cada uma das latas, em relação à sua capacidade, após essa divisão é:

1. 1/3.
2. 5/8.
3. 5/6.
4. 4/3.
5. 5/2.

04. (UECE) Seja n um número inteiro positivo.

Se os três menores divisores positivos de n são os números 1, 3 e 13, e se a soma dos três maiores divisores de n é igual a 3905, então, n é igual a

1. 2535.
2. 2847.
3. 2769.
4. 2028.

05. (UPE) Rodrigo estava observando o pisca-pisca do enfeite natalino de sua casa. Ele é composto por lâmpadas nas cores amarelo, azul, verde e vermelho. Rodrigo notou que lâmpadas amarelas acendem a cada 45 segundos, as lâmpadas verdes, a cada 60 segundos, as azuis, a cada 27 segundos, e as vermelhas só acendem quando as lâmpadas das outras cores estão acesas ao mesmo tempo. De quantos em quantos minutos, as lâmpadas vermelhas acendem?

1. 6
2. 9
3. 12
4. 15
5. 18

06. (UECE) O número de divisores inteiros e positivos do número 2018² - 2017² é

1. 8.
2. 14.
3. 10.
4. 12.

07. (PUC-PR) Um estagiário recebeu a tarefa de organizar documentos em três arquivos. No primeiro arquivo, havia apenas 42 contratos de locação; no segundo arquivo, apenas 30 contratos de compra e venda; no terceiro arquivo, apenas 18 laudos de avaliação de imóveis. Ele foi orientado a colocar os documentos em pastas, de modo que todas as pastas devem conter a mesma quantidade de documentos. Além de não poder mudar algum documento do seu arquivo original, deveria colocar na menor quantidade possível de pastas.

O número mínimo de pastas que ele pode usar é:

1. 13.
2. 15.
3. 26.
4. 28.
5. 30.

08. (UECE) A quantidade de números inteiros positivos com quatro algarismos distintos que são múltiplos de quatro é

1. 1136.
2. 1114.
3. 1126.
4. 1120.

09. (ESA) Uma herança de R$ 193.800,00 será repartida integralmente entre três herdeiros em partes diretamente proporcionais às suas respectivas idades: 30 anos, 35 anos e 37 anos.

O herdeiro mais velho receberá:

1. R$ 70.500,00
2. R$ 70.300,00
3. R$ 57.000,00
4. R$ 66.500,00
5. R$ 90.300,00

10. (UECE) Seja n o número obtido como a soma dos inversos multiplicativos dos números primos positivos que são fatores do número 195. Se p é o inverso multiplicativo de n, então, p cumpre a condição

1. 1,5 < p < 1,7.
2. 1,4 < p < 1,6.
3. 1,8 < p < 1,9.
4. 1,7 < p < 1,8.

11. (PUC-RS) O Portão de Brandemburgo, em Berlim, possui cinco entradas, cada uma com 11 metros de comprimento. Tales passou uma vez pela primeira porta, duas vezes pela segunda e assim sucessivamente, até passar cinco vezes pela quinta.

Então, ele percorreu _______ metros.

1. 55
2. 66
3. 165
4. 275
5. 330

12. (UDESC) A soma de todos os números naturais múltiplos de 9 que são formados por quatro algarismos deixa como resto:

1. 0 na divisão por 6.
2. 1 na divisão por 3.
3. 3 na divisão por 4.
4. 2 na divisão por 5.
5. 4 na divisão por 10.

13. (UEMG) Para realizar uma pesquisa sobre animais marinhos, um grupo de 18 estudantes gasta 20 dias.

Para realizar a mesma pesquisa durante 12 dias, com estudantes com a mesma capacidade de trabalho dos anteriores, o número de estudantes que deve compor esse grupo é

1. 30.
2. 20.
3. 36.
4. 16.

14. (IME) O menor número natural ímpar que possui o mesmo número de divisores que 1800 está no intervalo:

1. [1,16000]
2. [16001,17000]
3. [17001,18000]
4. [18001,19000]
5. [19001, ∞)

15. (UMC-SP) O número de elementos do conjunto dos divisores primos de 60 é:

1. 3
2. 4
3. 5
4. 10