Sistemas Lineares
Gabarito de Matemática sobre o tema Sistemas Lineares com questões de Vestibulares.
1. (Unesp) Uma pessoa quer trocar suas cédulas de 100 reais por cédulas de 5, 10 e 50 reais, recebendo cédulas de todos esses valores e o maior número possível de cédulas de 50 reais. Nessas condições, qual é o número mínino de cédulas que ela poderá receber?
- 8
- 9
- 10
- 11
- 12
Resposta: B
Resolução: Maior n° possível de cédulas de R$50,00. Não pode ter 4 notas de 50 reais, não teria como ter cédulas de 10 e 5.
cédulas de 50 reais = 3 ( 150,00 )
Sobram 50 reais, não poderia ter 5 notas de 10, porque faltaria no cálculo notas de 5.
cédulas de 10 reais = 4
Sobram 10 reais = 2 notas de 5 reais.
Cálculo
50 + 50 + 50 + 10 + 10 + 10 + 10 + 5 + 5 = 9 notas
Resposta: 9 cédulas.
2. (UFPB) Fernando foi a um caixa eletrônico e fez um saque em cédulas de três tipos diferentes: R$ 20,00, R$ 10,00 e R$ 5,00. Sabe-se que ele retirou 14 cédulas e que a quantia foi a mesma para cada tipo de cédula. A quantia sacada por Fernando foi:
- R$ 120,00
- R$ 150,00
- R$ 180,00
- R$ 210,00
- R$ 240,00
Resposta: A
Resolução: R$ 120,00
3. (UESP) Se o terno (x0, y0, z0) é a solução do sistema abaixo, então 3×0 + 5y0 + 4z0 é igual a:

- -8
- -7
- -6
- -5
- -4
Resposta: B
Resolução: o método mais fácil de conseguir a resposta é somar as equações;
3x+z = -5
(x +z + y=-2)
( -z +2y=-3)
some as duas equações sublinhadas
3x+z+0y=-5
0x-z+2y=-3
------------------
{3x+2y=-8}
agora some as duas equações entre parenteses
1x+1z+1y=-2
0x-1z+2y=-3
--------------------
{x+3y=-5}
então você soma as duas equações entre chaves, mas para isso você tem que pensar como zerar o x ou o y.para
que isso ocorra o certo seria multiplicar a ultima expressão por -3.
3x+2y=-8⇔ 3x+2y=-8
1x+3y=-5 ⇒multiplicar por -3⇒-3x-9y=15
--------------------------------------------------------------------
-7y=7⇔y=-1
como descobrimos o valor de y podemos substituir em uma das equações entre chaves:
x+3y=-5⇔x+3.-1=-5⇒x-3=-5⇒x=-2
Então substitua os valores em uma das equações sublinhadas
3x+z=-5⇒3.-2+z=-5⇒-6+z=-5⇒z=1
agora sabemos os termos(-2,-1,1)
e podemos substituir na equação 3xo+5yo+4zo
3.-2+5.-+4.1⇒-6-5+4⇒-7⇒b
4. (UEL) O sistema abaixo, de incógnitas x e y, é:
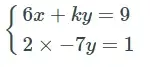
- impossível, para todo k real diferente de -21;
- possível e indeterminado, para todo k real diferente de -63;
- possível e determinado, para todo k real diferente de -21;
- possível e indeterminado, para todo k real diferente de -3;
- possível e determinado, para todo k real diferente de -1 e -63.
Resposta: C
Resolução: possível e determinado, para todo k real diferente de -21;
05. (Unesp) Uma coleção de artrópodes é formada por 36 exemplares, todos eles íntegros e que somam, no total da coleção, 113 pares de patas articuladas. Na coleção não há exemplares das classes às quais pertencem o caranguejo, a centopeia e o piolho-de-cobra.
- Arachnida, com maior número de exemplares da classe Arachnida.
- Diplopoda, com maior número de exemplares da classe Diplopoda.
- Chilopoda, com igual número de exemplares de cada uma dessas classes.
- Arachnida, com maior número de exemplares da classe Insecta.
- Chilopoda, com maior número de exemplares da classe Chilopoda.
Resposta: D
Resolução: Primeiro vamos pensar que o texto nos deu que temos 36 artrópodes com 113 patas, segundo as espécies citadas teremos artrópodes dos seguintes filos: Crustáceos (caranguejos), Diplópodas (piolho-de-cobra) e os Quilópodas (centopeia). Assim conseguimos ver que a coleção tem somente Insetos (3 pares de patas) e Aracnídeos (4 pares de patas).
Para descobrirmos qual tem mais podemos fazer uma conta matemática bem simples :
19 aracnídeos + 17 insetos = 254 patas (ou seja, 127 pares de patas).
No enunciado nos diz que temos 113 patas , com isso podemos perceber que temos mais insetos do que aracnídeos.
6. (UECE) Se x, y e z constitui a solução do sistema linear

então o produto x. y. z é igual a
- -4
- -8
- -2
- -6
Resposta: C
Resolução: Resolvendo de 2 em 2:
1)
x+y+z=1
x+2y+3z=-2 x(-1)
x+y+z=1
-x-2y-3z =2 ( Soma as duas equações)
0 - y -2z = 3
-y - 2z = 3
2)
x+2y+3z=-2
x+4y+5z=-4 x(-1)
x+2y+3z=-2
-x-4y-5z=4 (Soma as duas)
0 -2y -2z =2
-2y-2z=2
-y-z=1
Se -y-2z =3, então y=-2z-3
Logo, -(-2z-3) -z =1
2z + 3 -z = 1
z =-2
y = -2(-2)-3
y = 4-3 = 1
x+y+z=1
Então, x+ 1+ -2=1
x=1+2-1
x=2
Resposta: x, y, z= 2, 1, -2
7. (UFRGS) O sistema de equações

- nenhuma solução.
- uma solução.
- duas soluções.
- três soluções.
- infinitas soluções
Resposta: B
Resolução:
8. (UPE) Em uma floricultura, é possível montar arranjos diferentes com rosas, lírios e margaridas. Um arranjo com 4 margaridas, 2 lírios e 3 rosas custa 42 reais. No entanto, se o arranjo tiver uma margarida, 2 lírios e uma rosa, ele custa 20 reais. Entretanto, se o arranjo tiver 2 margaridas, 4 lírios e uma rosa, custará 32 reais. Nessa floricultura, quanto custará um arranjo simples, com uma margarida, um lírio e uma rosa?
- 5 reais
- 8 reais
- 10 reais
- 15 reais
- 24 reais
Resposta: D
Resolução:
9. (Ufrgs) Inovando na forma de atender aos clientes, um restaurante serve alimentos utilizando pratos de três cores diferentes: verde, amarelo e branco. Os pratos da mesma cor custam o mesmo valor. Na mesa A, foram consumidos os alimentos de 3 pratos verdes, de 2 amarelos e de 4 brancos, totalizando um gasto de R$ 88,00. Na mesa B, foram consumidos os alimentos de 2 pratos verdes e de 5 brancos, totalizando um gasto de R$ 64,00. Na mesa C, foram consumidos os alimentos de 4 pratos verdes e de 1 amarelo, totalizando um gasto de R$ 58,00.
Comparando o valor do prato branco com o valor dos outros pratos, verifica-se que esse valor é
- 80% do valor do prato amarelo.
- 75% do valor do prato amarelo.
- 50% do valor do prato verde.
- maior que o valor do prato verde.
- a terça parte do valor da soma dos valores dos outros pratos.
Resposta: A
Resolução:
10. (Ufsm) Num determinado mês, em uma unidade de saúde, foram realizadas 58 hospitalizações para tratar pacientes com as doenças A, B e C. O custo total em medicamentos para esses pacientes foi de R$39.200,00.
Sabe-se que, em média, o custo por paciente em medicamentos para a doença A é R$450,00, para a doença B é R$800,00 e para a doença C é R$1.250,00. Observa-se também que o número de pacientes com a doença A é o triplo do número de pacientes com a doença C. Se a, b e c representam, respectivamente, o número de pacientes com as doenças A, B e C, então o valor de a - b - c é igual a
- 14.
- 24.
- 26.
- 36.
- 58
Resposta: A
Resolução: Sabe-se que, em média, o custo por paciente em medicamentos
para a doença A é R$450,00
para a doença B é R$800,00
para a doença C é R$1.250,00.
450A + 800B + 1250C = 39.200 ( divide TUDO por 50) facilitar 9A + 16B + 25C = 784
Observa-se também que o número de pacientes com a doença A é o triplo do número de pacientes com a doença C.
SISTEMA com 3 variaveis
{ A + B + C = 58
{9A + 16B + 25C = 784
A + B + C = 58 (-16) multiplica
-16A-16B - 16C = - 928 junta
- 16A - 16B - 16C = -928
9A + 16B + 25C = 784 SOMA
-------------------------------------------
- 7A 0 + 9C = - 144
- 7A + 9C = - 144 ( sendo A = 3C) ( A é o triplo de C)
- 7(3C) + 9C = - 144
- 21C + 9C = - 144
- 12C = - 144
C = - 144/-12
C = + 144/12
C = 12 ( achar o valor de (A))
A = 3C
A = 3(12)
A = 36 ( achar o valor de (B))
A + B + C = 58
36 + B + 12 = 58
36 + 12 + B = 58
48 + B = 58
B = 58 - 48
B = 10
assim
A = 36
B = 10
C = 12
então o valor de a - b - c é igual a:
A - B - C =
36 - 10 - 12 =
36 - 22 = 14 ( resposta)