Plano Cartesiano

01. (UEA) Considere as equações I, II e III.

(I) x + y + 3 = 0

(II) x² + 2y + 2 = 0

(III) x² + y² – 5 = 0

No plano cartesiano, as representações gráficas das equações I, II e III correspondem, respectivamente, a

1. circunferência, parábola e reta.
2. parábola, reta e circunferência.
3. reta, circunferência e parábola.
4. circunferência, reta e parábola.
5. reta, parábola e circunferência.

02. (Fuvest) A região hachurada do plano cartesiano xOy contida no círculo de centro na origem O e raio 1, mostrada na figura, pode ser descrita por

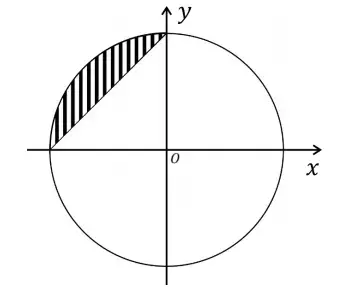
A região hachurada do plano cartesiano xOy contida no círculo de centro na origem O e raio 1, mostrada na figura, pode ser descrita por

Note e adote:

O círculo de centro O e raio 1 é o conjunto de todos os pontos do plano que estão a uma distância de O menor do que ou igual a 1.

1. {(x,y); x² + y² ≤ 1 e y - x ≤ 1 }.
2. {(x,y); x² + y² ≥ 1 e y + x ≥ 1 }.
3. {(x,y); x² + y² ≤ 1 e y - x ≥ 1 }.
4. {(x,y); x² + y² ≤ 1 e y + x ≥ 1 }.
5. {(x,y); x² + y² ≥ 1 e y + x ≤ 1 }.

03. (Fuvest) Um ponto (x ,y) do plano cartesiano pertence ao conjunto F se é equidistante dos eixos OX e OY e pertence ao círculo de equação x² + y² - 2x - 6y + 2 = 0.

É correto afirmar que F

1. é um conjunto vazio.
2. tem exatamente 2 pontos, um no primeiro quadrante e outro no segundo quadrante.
3. tem exatamente 2 pontos, ambos no primeiro quadrante.
4. tem exatamente 3 pontos, sendo dois no primeiro quadrante e outro no segundo quadrante.
5. tem exatamente 4 pontos, sendo dois no primeiro quadrante e dois no segundo quadrante.

04. (Unicamp) Sabendo que 𝑐 é um número real, considere, no plano cartesiano, a circunferência de equação x² + y² = 2𝑐𝑥. Se o centro dessa circunferência pertence à reta de equação x + 2y = 3, então seu raio é igual a

1. √2.
2. √3.
3. 2.
4. 3.

05. (Famerp) Em um plano cartesiano, dois vértices de um triângulo equilátero estão sobre a reta de equação y = 2x – 2. O terceiro vértice desse triângulo está sobre a reta de equação y = 2x + 2. A altura desse triângulo, na mesma unidade de medida dos eixos cartesianos ortogonais, é igual a

1. 4√3/5
2. 3√3/4
3. 2√5/5
4. 4√5/5
5. √3/2

06. (FAMERP) A figura indica os gráficos de uma reta r e uma senoide s, de equações y = 5/2 e y = 1 + 3 sen (2x), em um plano cartesiano de eixos ortogonais.

Sendo P um ponto de intersecção dos gráficos, conforme mostra a figura, sua abscissa, convertida para graus, é igual a

1. 275º
2. 240º
3. 225º
4. 210º
5. 195º

07. (Albert Einstein) O esquema a seguir é uma representação simplificada de um raio X usado em um aparelho de tomografia computadorizada axial para compor imagens de objetos.

No plano cartesiano com origem no centro do objeto, indicado na figura, a reta do raio X tem equação 3x + 4y – 12 = 0.

A distância d, entre o centro do objeto e a reta do raio X, na unidade do plano cartesiano, é igual a

1. 12/5
2. 21/10
3. 11/5
4. 9/4
5. 5/2

08. (UFPR) Considere a circunferência B, cuja equação no plano cartesiano é x² + y² − 8x + 10y + 21 = 0.

Qual das equações abaixo descreve uma circunferência que tangencia B?

1. (x + 1)² + (y − 2)² = 15.
2. (x + 2)² + (y + 2)² = 5.
3. (x − 3)² + (y − 1)² = 3
4. (x − 7)² + (y − 2)² = 10.
5. (x + 3)² + (y + 2)² = 9.

09. (FAMEMA) Em um plano cartesiano, seja r a reta de equação x - 3y + 6 = 0. A reta s é perpendicular à reta r e delimita, com os eixos coordenados, no primeiro quadrante, um triângulo de área 128/3.

O ponto de interseção de r e s tem abscissa

1. 23/5
2. 21/5
3. 18/5
4. 19/5
5. 24/5

10. (UERJ) No plano cartesiano, está representada a circunferência de centro P e raio 2.

O ponto Q da circunferência, que é o mais distante da origem, tem coordenadas iguais a:

1. (28/5, 21/5)
2. (31/5, 26/5)
3. (33/5, 29/5)
4. (36/5, 37/5)