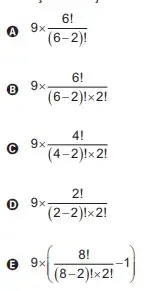Análise Combinatória I
Lista de 15 exercícios de Matemática com gabarito sobre o tema Análise Combinatória I com questões do Enem.
01. (Enem 2023) Ao realizar o cadastro em um aplicativo de investimentos, foi solicitado ao usuário que criasse uma senha, sendo permitido o uso somente dos seguintes caracteres:
• algarismos de 0 a 9;
• 26 letras minúsculas do alfabeto;
• 26 letras maiúsculas do alfabeto;
• 6 caracteres especiais: !, @, #, $, *, &.
Três tipos de estruturas para senha foram apresentadas ao usuário:
• tipo I: formada por quaisquer quatro caracteres distintos, escolhidos dentre os permitidos;
• tipo II: formada por cinco caracteres distintos, iniciando por três letras, seguidas por um algarismo e, ao final, um caractere especial;
• tipo III: formada por seis caracteres distintos, iniciando por duas letras, seguidas por dois algarismos e, ao final, dois caracteres especiais.
Considerando P1, P2 e P3, e as probabilidades de se descobrirem ao acaso, na primeira tentativa, as senhas dos tipos I, II e III, respectivamente.
Nessas condições, o tipo de senha que apresenta a menor probabilidade de ser descoberta ao acaso, na primeira tentativa, é
- tipo I, pois p1 < p2 < p3.
- tipo I, pois tem menor quantidade de caracteres.
- tipo II, pois tem maior quantidade de letras.
- tipo III, pois p3 < p2 < p1.
- tipo III, pois tem maior quantidade de caracteres.
Resposta: A
Resolução:
02. (ENEM PPL 2021) Um diretor esportivo organiza um campeonato no qual haverá disputa de times em turno e returno, isto é, cada time jogará duas vezes com todos os outros, totalizando 380 partidas a serem disputadas.
Aquantidade de times (x) que faz parte desse campeonato pode ser calculada pela equação
- x - 380 - x²
- x² - x - 380
- x²-380
- 2x - x-380
- 2x - 380
Resposta: B
Resolução:
03. (ENEM 2022) Foram convidadas 32 equipes para um torneio de futebol, que foram divididas em 8 grupos com 4 equipes, sendo que, dentro de um grupo, cada equipe disputa uma única partida contra cada uma das demais equipes de seu grupo. A primeira e a segunda colocadas de cada grupo seguem para realizar as 8 partidas da próxima fase do torneio, chamada oitavas de final. Os vencedores das partidas das oitavas de final seguem para jogar as 4 partidas das quartas de final. Os vencedores das quartas de final disputam as 2 partidas das semifinais, e os vencedores avançam para a grande final, que define a campeã do torneio.
Pelas regras do torneio, cada equipe deve ter um período de descanso de, no mínimo, 3 dias entre dois jogos por ela disputados, ou seja, se um time disputar uma partida, por exemplo, num domingo, só poderá disputar a partida seguinte a partir da quinta-feira da mesma semana.
O número mínimo de dias necessários para a realização desse torneio é
- 22.
- 25.
- 28.
- 48.
- 64.
Resposta: B
Resolução:
04. (Enem 2022) Uma montadora de automóveis divulgou que oferta a seus clientes mais de 1 000 configurações diferentes de carro, variando o modelo, a motorização, os opcionais e a cor do veículo. Atualmente, ela oferece 7 modelos de carros com 2 tipos de motores: 1.0 e 1.6. Já em relação aos opcionais, existem 3 escolhas possíveis: central multimídia, rodas de liga leve e bancos de couro, podendo o cliente optar por incluir um, dois, três ou nenhum dos opcionais disponíveis.
Para ser fiel à divulgação feita, a quantidade mínima de cores que a montadora deverá disponibilizar a seus clientes é
- 8.
- 9.
- 11.
- 18.
- 24.
Resposta: B
Resolução:
05. (Enem 2022) Um prédio, com 9 andares e 8 apartamentos de 2 quartos por andar, está com todos os seus apartamentos à venda. Os apartamentos são identificados por números formados por dois algarismos, sendo que a dezena indica o andar onde se encontra o apartamento, e a unidade, um algarismo de 1 a 8, que diferencia os apartamentos de um mesmo andar. Quanto à incidência de sol nos quartos desses apartamentos, constatam-se as seguintes características, em função de seus números de identificação:
• naqueles que finalizam em 1 ou 2, ambos os quartos recebem sol apenas na parte da manhã;
• naqueles que finalizam em 3, 4, 5 ou 6, apenas um dos quartos recebe sol na parte da manhã;
• naqueles que finalizam em 7 ou 8, ambos os quartos recebem sol apenas na parte da tarde.
Uma pessoa pretende comprar 2 desses apartamentos em um mesmo andar, mas quer que, em ambos, pelo menos um dos quartos receba sol na parte da manhã.
De quantas maneiras diferentes essa pessoa poderá escolher 2 desses apartamentos para compra nas condições desejadas?
Resposta: B
Resolução:
06. (Enem 2020) Um hotel de 3 andares está sendo construído. Cada andar terá 100 quartos. Os quartos serão numerados de 100 a 399 e cada um terá seu número afixado à porta. Cada número será composto por peças individuais, cada uma simbolizando um único algarismo.
Qual a quantidade mínima de peças, simbolizando o algarismo 2, necessárias para identificar o número de todos os quartos?
- 160
- 157
- 130
- 120
- 60
Resposta: A
Resolução:
07. (Enem 2020) Os gráficos representam a produção de peças em uma indústria e as horas trabalhadas dos funcionários no período de cinco dias. Em cada dia, o gerente de produção aplica uma metodologia diferente de trabalho. Seu objetivo é avaliar a metodologia mais eficiente para utilizá-la como modelo nos próximos períodos. Sabe-se que, neste caso, quanto maior for a razão entre o número de peças produzidas e o número de horas trabalhadas, maior será a eficiência da metodologia.
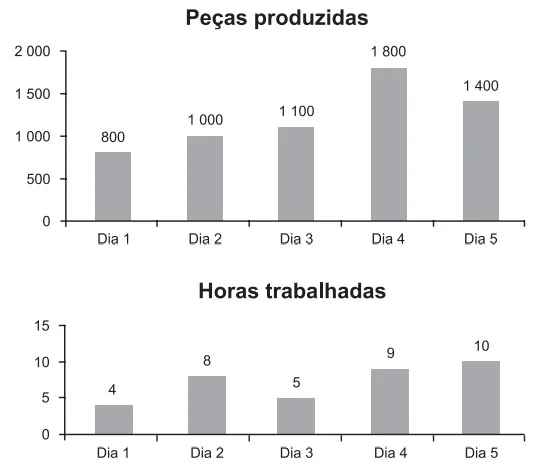
Em qual dia foi aplicada a metodologia mais eficiente?
- 1
- 2
- 3
- 4
- 5
Resposta: C
Resolução:
08. (Enem 2020) Nos livros Harry Potter, um anagrama do nome do personagem “TOM MARVOLO RIDDLE” gerou a frase “I AM LORD VOLDEMORT”.
Suponha que Harry quisesse formar todos os anagramas da frase “I AM POTTER”, de tal forma que as vogais e consoantes aparecessem sempre intercaladas, e sem considerar o espaçamento entre as letras.
Nessas condições, o número de anagramas formados é dado por
- 9!
- 4! 5!
- 2 x 4! 5!
Resposta: E
Resolução:
09. (Enem 2020) Três amigos, André, Bernardo e Carlos, moram em um condomínio fechado de uma cidade. O quadriculado representa a localização das ruas paralelas e perpendiculares, delimitando quadras de mesmo tamanho nesse condomínio, em que nos pontos A, B e C estão localizadas as casas de André, Bernardo e Carlos, respectivamente.
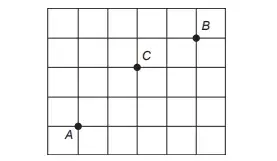
André deseja deslocar-se da sua casa até a casa de Bernardo, sem passar pela casa de Carlos, seguindo ao longo das ruas do condomínio, fazendo sempre deslocamentos para a direita (→) ou para cima (↑), segundo o esquema da figura.
O número de diferentes caminhos que André poderá utilizar para realizar o deslocamento nas condições propostas é
- 4
- 14
- 17
- 35
- 48
Resposta: C
Resolução:
10. (Enem Digital 2020) Eduardo deseja criar um e-mail utilizando um anagrama exclusivamente com as sete letras que compõem o seu nome, antes do símbolo @. O e-mail terá a forma *******@site.com.br e será de tal modo que as três letras “edu” apareçam sempre juntas e exatamente nessa ordem. Ele sabe que o e-mail eduardo@site.com.br já foi criado por outro usuário e que qualquer outro agrupamento das letras do seu nome forma um e-mail que ainda não foi cadastrado. De quantas maneiras Eduardo pode criar um e-mail desejado?
- 59
- 60
- 118
- 119
- 120
Resposta: D
Resolução:
11. (Enem Digital 2020) “1, 2, 3, GOL, 5, 6, 7, GOL, 9, 10, 11, GOL, 13, GOL, 15, GOL, 17, 18, 19, GOL, 21, 22, 23, GOL, 25, ...”
Para a Copa do Mundo de Futebol de 2014, um bar onde se reuniam amigos para assistir aos jogos criou uma brincadeira. Um dos presentes era escolhido e tinha que dizer, numa sequência em ordem crescente, os números naturais não nulos, trocando os múltiplos de 4 e os números terminados em 4 pela palavra GOL. A brincadeira acabava quando o participante errava um termo da sequência.
Um dos participantes conseguiu falar até o número 103, respeitando as regras da brincadeira.
O total de vezes em que esse participante disse a palavra GOL foi
- 20.
- 28.
- 30.
- 35.
- 40.
Resposta: C
Resolução:
12. (Enem Digital 2020) Um modelo de telefone celular oferece a opção de desbloquear a tela usando um padrão de toques como senha.

Os toques podem ser feitos livremente nas 4 regiões numeradas da tela, sendo que o usuário pode escolher entre 3, 4 ou 5 toques ao todo.
Qual expressão representa o número total de códigos existentes?
- 45 - 44 - 43
- 45 + 44 + 43
- 45 x 44 x 43
- (!4)5
- 4 5
Resposta: B
Resolução:
13. (Enem PPL 2020) A prefeitura de uma cidade está renovando os canteiros de flores de suas praças. Entre as possíveis variedades que poderiam ser plantadas, foram escolhidas cinco: amor-perfeito, cravina, petúnia, margarida e lírio. Em cada um dos canteiros, todos com composições diferentes, serão utilizadas somente três variedades distintas, não importando como elas serão dispostas.
Um funcionário deve determinar os trios de variedades de flores que irão compor cada canteiro.
De acordo com o disposto, a quantidade de trios possíveis é dada por
- 5
- 5 ∙ 3
- 5!/(5 − 3)!
- 5!/(5 − 3)!2!
- 5!/(5 − 3)!3!
Resposta: E
Resolução:
14. (Enem PPL 2020) O governador de um estado propõe a ampliação de investimentos em segurança no transporte realizado por meio de trens. Um estudo para um projeto de lei prevê que se tenha a presença de três agentes mulheres, distribuídas entre os 6 vagões de uma composição, de forma que duas dessas agentes não estejam em vagões adjacentes, garantindo assim maior segurança aos usuários.
Disponível em: sisgraph.com.br. Acesso em: 29 jan. 2015 (adaptado).
A expressão que representa a quantidade de maneiras distintas das três agentes serem distribuídas nos vagões é
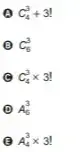
Resposta: C
Resolução:
15. (Enem PPL 2020) Um determinado campeonato de futebol, composto por 20 times, é disputado no sistema de pontos corridos. Nesse sistema, cada time joga contra todos os demais times em dois turnos, isto é, cada time joga duas partidas com cada um dos outros times, sendo que cada jogo pode terminar empatado ou haver um vencedor.
Sabendo-se que, nesse campeonato, ocorreram 126 empates, o número de jogos em que houve ganhador é igual a
- 64.
- 74.
- 254.
- 274.
- 634
Resposta: C
Resolução: