Sólidos de Revolução

01. (Enem 2023) A foto mostra a construção de uma cisterna destinada ao armazenamento de água. Uma cisterna como essa, na forma de cilindro circular reto com 3 m² de área da base, foi abastecida por um curso-d'água com vazão constante. O seu proprietário registrou a altura do nível da água no interior da cisterna durante o abastecimento em diferentes momentos de um mesmo dia, conforme o quadro.

Qual foi a vazão, em metro cúbico por hora, do curso-d'água que abastece a cisterna?

1. 0,3
2. 0,5
3. 0,9
4. 1,8
5. 2,7

02. (Enem PPL 2022) Uma indústria planeja produzir caixa-d’água, em formato cilíndrico, com 1 m de altura, capaz de armazenar 0,4 m3 de água.

A medida do raio da base dessa caixa-d’água, em metro, deve ser

1. 0,2/π
2. 0,4/π
3. √ 0,2/π
4. √ 0,4/π
5. √ 1,2/π

03. (Enem 2022) Uma loja comercializa cinco modelos de caixas-d'água (l, Il, III, IV e V), todos em formato de cilindro reto de base circular. Os modelos II,III, IV e V têm as especificações de suas dimensões dadas em relação às dimensões do modelo I, cuja profundidade é P e área da base é Ab, como segue:

• modelo II: o dobro da profundidade e a metade da área da base do modelo I;

• modelo III: o dobro da profundidade e a metade do raio da base do modelo I;

• modelo IV: a metade da profundidade e o dobro da área da base do modelo I;

• modelo V: a metade da profundidade e o dobro do raio da base do modelo I.

Uma pessoa pretende comprar nessa loja o modelo de caixa-d água que ofereça a maior capacidade volumétrica

O modelo escolhido deve ser o

1. I.
2. II.
3. III.
4. IV.
5. V.

04. (Enem 2022) Peças metálicas de aeronaves abandonadas em aeroportos serão recicladas. Uma dessas peças é maciça e tem o formato cilíndrico, com a medida do raio da base igual a 4 cm e a da altura igual a 50 cm. Ela será derretida, e o volume de metal resultante será utilizado para a fabricação de esferas maciças com diâmetro de 1 cm, a serem usadas para confeccionar rolamentos. Para estimar a quantidade de esferas que poderão ser produzidas a partir de cada uma das peças cilíndricas, admite-se que não ocorre perda de material durante o processo de derretimento.

Quantas dessas esferas poderão ser obtidas a partir de cada peça cilíndrica?

1. 800
2. 1 200
3. 2 400
4. 4 800
5. 6 400

05. (Enem 2021) Uma pessoa comprou uma caneca para tomar sopa, conforme ilustração.

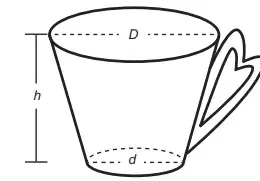
Sabe-se que 1 cm³ = 1 mL e que o topo da caneca é uma circunferência de diâmetro (D) medindo 10 cm, e a base é um círculo de diâmetro (d) medindo 8 cm. Além disso, sabe-se que a altura (h) dessa caneca mede 12 cm (distância entre o centro das circunferências do topo e da base).

Utilize 3 como aproximação para π.

Qual é a capacidade volumétrica, em mililitro, dessa caneca?

1. 216
2. 408
3. 732
4. 2 196
5. 2 928

06. (Enem 2021) Um povoado com 100 habitantes está passando por uma situação de seca prolongada e os responsáveis pela administração pública local decidem contratar a construção de um reservatório. Ele deverá ter a forma de um cilindro circular reto, cuja base tenha 5 metros de diâmetro interno, e atender à demanda de água da população por um período de exatamente sete dias consecutivos. No oitavo dia, o reservatório vazio é completamente reabastecido por carros-pipa.

Considere que o consumo médio diário por habitante é de 120 litros de água. Use 3 como aproximação para π.

Nas condições apresentadas, o reservatório deverá ser construído com uma altura interna mínima, em metro, igual a

1. 1,12.
2. 3,10.
3. 4,35.
4. 4,48.
5. 5,60.

07. (Enem 2020) Uma loja de materiais de construção vende dois tipos de caixas-d’água: tipo A e tipo B. Ambas têm formato cilíndrico e possuem o mesmo volume, e a altura da caixa-d’água do tipo B é igual a 25% da altura da caixa-d’água do tipo A.

Se R denota o raio da caixa-d’água do tipo A, então o raio da caixa-d’água do tipo B é

1. $\frac{R}{2}$
2. 2R
3. 4R
4. 5R
5. 16R

08. (Enem 2015) Em uma confeitaria, um cliente comprou um cupcake (pequeno bolo no formato de um tronco de cone regular mais uma cobertura, geralmente composta por um creme), semelhante ao apresentado na figura:

Como o bolinho não seria consumido no estabelecimento, o vendedor verificou que as caixas disponíveis para embalar o doce eram todas em formato de blocos retangulares, cujas medidas estão apresentadas no quadro:

A embalagem mais apropriada para armazenar o doce, de forma a não deformá-lo e com menor desperdício de espaço na caixa, é

1. I
2. II
3. III
4. IV
5. V

09. (Enem 2019) Uma construtora pretende conectar um reservatório central (R_c) em formato de um cilindro, com raio interno igual a 2 m e altura interna igual a 3,30 m, a quatro reservatórios cilíndricos auxiliares (R₁, R₂, R₃ e R₄), os quais possuem raios internos e alturas internas medindo 1,5 m

As ligações entre o reservatório central e os auxiliares são feitas por canos cilíndricos com 0,10 m de diâmetro interno e 20 m de comprimento, conectados próximos às bases de cada reservatório. Na conexão de cada um desses canos com o reservatório central há registros que liberam ou interrompem o fluxo de água.

No momento em que o reservatório central está cheio e os auxiliares estão vazios, abrem-se os quatro registros e, após algum tempo, as alturas das colunas de água nos reservatórios se igualam, assim que cessa o fluxo de água entre eles, pelo princípio dos vasos comunicantes.

A medida, em metro, das alturas das colunas de água nos reservatórios auxiliares, após cessar o fluxo de água entre eles, é

1. 1,44
2. 1,16
3. 1,10
4. 1,00
5. 0,95

10. (Enem 2023) Um artista plástico esculpe uma escultura a partir de um bloco de madeira de lei, em etapas. Inicialmente, esculpe um cone reto com 36 cm de altura e diâmetro da base medindo 18 cm. Em seguida, remove desse cone um cone menor, cujo diâmetro da base mede 6 cm, obtendo, assim, um tronco de cone, conforme ilustrado na figura.

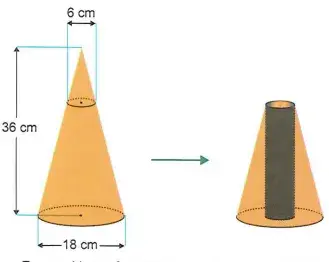
Em seguida, perfura esse tronco de cone, removendo um cilindro reto, de diâmetro 6 cm, cujo eixo de simetria é o mesmo do cone original. Dessa forma, ao final, a escultura tem a forma de um tronco de cone com uma perfuração cilíndrica de base a base.

O tipo de madeira utilizada para produzir essa escultura tem massa igual a 0,6 g por centímetro cúbico de volume. Utilize 3 como aproximação para π.

Qual é a massa, em grama, dessa escultura?

1. 1 198,8
2. 1 296,0
3. 1 360,8
4. 4 665,6
5. 4 860,0

11. (Enem 2017) Para a Olimpíada de 2012, a piscina principal do Centro Aquático de Londres, medindo 50 metros de comprimento, foi remodelada para ajudar os atletas a melhorar suas marcas. Observe duas das melhorias:

A capacidade da piscina em destaque, em metro cúbico, é igual a

1. 3 750.
2. 1 500.
3. 1 250.
4. 375.
5. 150.

12. (Enem PPL 2022) Um novo produto, denominado bolo de caneca no micro-ondas, foi lançado no mercado com o objetivo de atingir ao público que não tem muito tempo para cozinhar. Para prepará-lo, uma pessoa tem à sua disposição duas opções de canecas, apresentadas na figura.

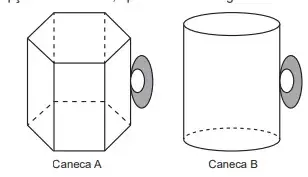
A caneca A tem formato de um prisma reto regular hexagonal de lado L = 4 cm, e a caneca B tem formato de um cilindro circular reto de diâmetro d = 6 cm. Sabe-se que ambas têm a mesma altura h = 10 cm, e que essa pessoa escolherá a caneca com maior capacidade. Considere π = 3,1 e π = 1,7

A medida da capacidade, em centímetro cúbico, da caneca escolhida é

1. 186
2. 279
3. 408
4. 816
5. 1 116

13. (Enem PPL 2020) Um piscicultor cria uma espécie de peixe em um tanque cilíndrico. Devido às características dessa espécie, o tanque deve ter, exatamente, 2 metros de profundidade e ser dimensionado de forma a comportar 5 peixes para cada metro cúbico de água. Atualmente, o tanque comporta um total de 750 peixes. O piscicultor deseja aumentar a capacidade do tanque para que ele comporte 900 peixes, mas sem alterar a sua profundidade. Considere 3 como aproximação para.

O aumento da medida do raio do tanque, em metro, deve ser de

1. √30 − 5
2. √30 − 5/2
3. 5
4. 5/2
5. 15/2