Probabilidade I

01. (Enem 2023) Em um colégio público, a admissão no primeiro ano se dá por sorteio. Neste ano há 55 candidatos, cujas inscrições são numeradas de 01 a 55. O sorteio de cada número de inscrição será realizado em etapas, utilizando-se duas urnas. Da primeira urna será sorteada uma bola, dentre bolas numeradas de 0 a 9, que representará o algarismo das unidades do número de inscrição a ser sorteado e, em seguida, da segunda urna, será sorteada uma bola para representar o algarismo das dezenas desse número. Depois do primeiro sorteio, e antes de se sortear o algarismo das dezenas, as bolas que estarão presentes na segunda urna serão apenas aquelas cujos números formam, com o algarismo já sorteado, um número de 01 a 55.

As probabilidades de os candidatos de inscrição número 50 e 02 serem sorteados são, respectivamente,

1. 1/50 e 1/60
2. 1/50 e 1/50
3. 1/50 e 1/10
4. 1/55 e 1/54
5. 1/100 e 1/100

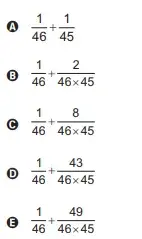
02. (Enem 2023) Visando atrair mais clientes, o gerente de uma loja anunciou uma promoção em que cada cliente que realizar uma compra pode ganhar um voucher para ser usado em sua próxima compra. Para ganhar seu voucher, o cliente precisa retirar, ao acaso, uma bolinha de dentro de cada uma das urnas A e B disponibilizadas pelo gerente, nas quais há apenas bolinhas pretas e brancas. Atualmente, a probabilidade de se escolher, ao acaso, uma bolinha preta na urna A é igual a 20% e a probabilidade de se escolher uma bolinha preta na urna B é 25%. Ganha o voucher o cliente que retirar duas bolinhas pretas, uma de cada urna.

Com o passar dos dias, o gerente percebeu que, para a promoção ser viável aos negócios, era preciso ajustar a probabilidade de acerto do cliente sem alterar a regra da promoção. Para isso, resolveu alterar a quantidade de bolinhas brancas na urna B de forma que a probabilidade de um cliente ganhar o voucher passasse a ser menor ou igual a 1%. Sabe-se que a urna B tem 4 bolinhas pretas e que, em ambas as urnas, todas as bolinhas têm a mesma probabilidade de serem retiradas.

Qual é o número mínimo de bolinhas brancas que o gerente deve adicionar à urna B?

1. 20
2. 60
3. 64
4. 68
5. 80

03. (Enem 2023) Uma loja vende seus produtos de duas formas: à vista ou financiado em três parcelas mensais iguais. Para definir o valor dessas parcelas nas vendas financiadas, a loja aumenta em 20% o valor do produto à vista e divide esse novo valor por 3. A primeira parcela deve ser paga no ato da compra, e as duas últimas, em 30 e 60 dias após a compra.

Um cliente da loja decidiu comprar, de forma financiada, um produto cujo valor à vista é R$ 1 500,00.

Utilize 5,29 como aproximação para √28.

A taxa mensal de juros compostos praticada nesse financiamento é de

1. 6,7%
2. 10%
3. 20%
4. 21,5%
5. 23,3%

04. (Enem 2023) No alojamento de uma universidade, há alguns quartos com o padrão superior ao dos demais. Um desses quartos ficou disponível, e muitos estudantes se candidataram para morar no local. Para escolher quem ficará com o quarto, um sorteio será realizado. Para esse sorteio, cartões individuais com os nomes de todos os estudantes inscritos serão depositados em uma urna, sendo que, para cada estudante de primeiro ano, será depositado um único cartão com seu nome; para cada estudante de segundo ano, dois cartões com seu nome; e, para cada estudante de terceiro ano, três cartões com seu nome. Foram inscritos 200 estudantes de primeiro ano, 150 de segundo ano e 100 de terceiro ano. Todos os cartões têm a mesma probabilidade de serem sorteados.

Qual a probabilidade de o vencedor do sorteio ser um estudante de terceiro ano?

1. 1/2
2. 1/3
3. 1/8
4. 1/9
5. 3/8

05. (Enem 2022) A Word Series é a decisão do campeonato norte-americano de beisebol. Os dois times que chegam a essa fase jogam, entre si, até sete partidas. O primeiro desses times que completar quatro vitórias é declarado campeão.

Considere que, em todas as partidas, a probabilidade de qualquer um dos dois times vencer é sempre 1/2.

Qual é a probabilidade de o time campeão ser aquele que venceu a primeira partida da World Series?

1. 35/64
2. 40/64
3. 42/64
4. 44/64
5. 52/64

06. (Enem 2022) Em um jogo de bingo, as cartelas contêm 16 quadriculas dispostas em linhas e colunas. Cada quadricula tem impresso um número, dentre os inteiros de 1 a 50, sem repetição de número. Na primeira rodada, um número é sorteado, aleatoriamente, dentre os 50 possíveis. Em todas as rodadas, o número sorteado é descartado e não participa dos sorteios das rodadas seguintes. Caso o jogador tenha em sua cartela o número sorteado, ele o assinala na cartela. Ganha o jogador que primeiro conseguir preencher quatro quadrículas que formam uma linha, uma coluna ou uma diagonal, conforme os tipos de situações ilustradas na Figura 1

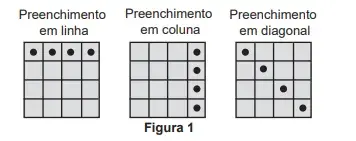
O jogo inicia e, nas quatro primeiras rodadas, foram sorteados os seguintes números: 03, 27, 07 e 48. Ao final da quarta rodada, somente Pedro possuía uma cartela que continha esses quatro números sorteados, sendo que todos os demais jogadores conseguiram assinalar, no máximo, um desses números em suas cartelas. Observe na Figura 2 o cartão de Pedro após as quatro primeiras rodadas.

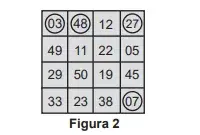
A probabilidade de Pedro ganhar o jogo em uma das duas próximas rodadas é

07. (Enem PPL 2022) Sete países americanos, Argentina, Brasil, Canadá, Chile, Estados Unidos, Paraguai e Uruguai; e sete países europeus, Portugal, Espanha, França, Inglaterra, Itália, Alemanha e Suíça, decidem criar uma comissão com representantes de oito desses países, objetivando criar políticas de incentivo e regulação do turismo entre eles. Na hipótese de criação da comissão, serão escolhidos aleatoriamente quatro representantes de países das Américas e quatro representantes de países europeus, não podendo estar na comissão dois representantes de um mesmo país.

Qual é a probabilidade de o Brasil e a França pertencerem a essa comissão?

1. 1/182
2. 1/49
3. 1/4
4. 1/13
5. 16/49

08. (Enem PPL 2022) Um curso preparatório para concursos tem duas turmas, A e B. Do total de alunos, 54% estão na turma A. A direção do curso decidiu pagar um bônus salarial aos professores dessas turmas, de acordo com a probabilidade de um aluno do curso, escolhido ao acaso, ser aprovado no concurso. Foi estabelecida a tabela que indica como o bônus seria definido.

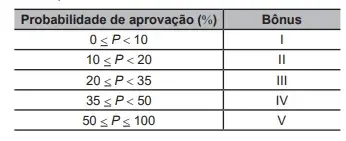
Para calcular a probabilidade desejada, foi aplicado um simulado anterior ao concurso. Nele, o percentual de aprovados da turma A foi de 25%, enquanto houve uma aprovação de 40% para os alunos da turma B.

Dessa forma, os professores desse curso devem receber o bônus

1. I.
2. II.
3. III.
4. IV.
5. V

09. (Enem 2021) O organizador de uma competição de lançamento de dardos pretende tornar o campeonato mais competitivo. Pelas regras atuais da competição, numa rodada, o Jogador lança 3 dardos e pontua caso acerte pelo menos um deles no alvo. O organizador considera que, em média, os jogadores têm, em cada lançamento, 1/2 de probabilidade de acertar um dardo no alvo.

A fim de tornar o jogo mais atrativo, planeja modificar as regras de modo que a probabilidade de um jogador pontuar em uma rodada seja igual ou superior a 9/10 Para isso, decide aumentar a quantidade de dardos a serem lançados em cada rodada.

Com base nos valores considerados pelo organizador da competição, a quantidade mínima de dardos que devem ser disponibilizados em uma rodada para tornar o jogo mais atrativo é

1. 2.
2. 4.
3. 6.
4. 9.
5. 10.

10. (Enem PPL 2021) A senha de um cofre é uma sequência formada por oito dígitos, que são algarismos escolhidos de O a 9. Ao inseri-la, o usuário se esqueceu dos dois últimos dígitos que formam essa senha, lembrando somente que esses dígitos são distintos.

Digitando ao acaso os dois dígitos esquecidos, a probabilidade de que o usuário acerte a senha na primeira tentativa é

1. 2/8
2. 1/90
3. 2/90
4. 1/100
5. 2/100

11. (Enem PPL 2021) Em uma fábrica de circuitos elétricos, há diversas linhas de produção e montagem. De acordo com o controle de qualidade da fábrica, as peças produzidas devem seguir um padrão. Em um processo produtivo, nem todas as peças produzidas são totalmente aproveitáveis, ou seja, há um percentual de peças defeituosas que são descartadas. Em uma linha de produção dessa fábrica, trabalham três máquinas, M1 M2 e M3 dia e noite. A máquina M1 produz 25% das peças, a máquina M2 produz 30% e a máquina M3 produz 45%. O percentual de peças defeituosas da máquina M1 é de 2%, da máquina M2 é de 3% e da máquina M3 é igual a 4%.

Aprobabilidade de uma peça defeituosa ter sido produzida pela máquina M2 é mais próxima de

1. 15,6%
2. 28,1%
3. 43,7%
4. 56,2%
5. 71,8%

12. (Enem 2020) O Estatuto do Idoso, no Brasil, prevê certos direitos às pessoas com idade avançada, concedendo a estas, entre outros benefícios, a restituição de imposto de renda antes dos demais contribuintes. A tabela informa os nomes e as idades de 12 idosos que aguardam suas restituições de imposto de renda. Considere que, entre os idosos, a restituição seja concedida em ordem decrescente de idade e que, em subgrupos de pessoas com a mesma idade, a ordem seja decidida por sorteio.

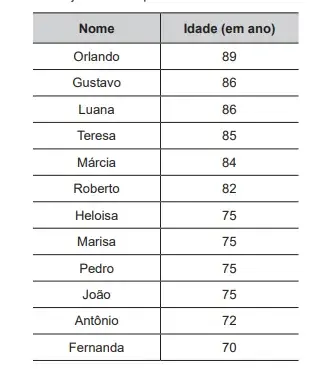
Nessas condições, a probabilidade de João ser a sétima pessoa do grupo a receber sua restituição é igual a

1. $\frac{1}{\mathrm{12}}$
2. $\frac{7}{\mathrm{12}}$
3. $\frac{1}{8}$
4. $\frac{5}{6}$
5. $\frac{1}{4}$

13. (Enem 2020) Amigo secreto é uma brincadeira tradicional nas festas de fim de ano. Um grupo de amigos se reúne e cada um deles sorteia o nome da pessoa que irá presentear. No dia da troca de presentes, uma primeira pessoa presenteia seu amigo secreto. Em seguida, o presenteado revela seu amigo secreto e o presenteia. A brincadeira continua até que todos sejam presenteados, mesmo no caso em que o ciclo se fecha. Dez funcionários de uma empresa, entre eles um casal, participarão de um amigo secreto. A primeira pessoa a revelar será definida por sorteio.

Qual é a probabilidade de que a primeira pessoa a revelar o seu amigo secreto e a última presenteada sejam as duas pessoas do casal?

1. $\frac{1}{5}$
2. $\frac{1}{\mathrm{45}}$
3. $\frac{1}{\mathrm{50}}$
4. $\frac{1}{\mathrm{90}}$
5. $\frac{1}{\mathrm{100}}$

14. (Enem 2020) Suponha que uma equipe de corrida de automóveis disponha de cinco tipos de pneu (I, II, III, IV, V), em que o fator de eficiência climática EC (índice que fornece o comportamento do pneu em uso, dependendo do clima) é apresentado:

EC do pneu I: com chuva 6, sem chuva 3;

EC do pneu II: com chuva 7, sem chuva –4;

EC do pneu III: com chuva –2, sem chuva 10;

EC do pneu IV: com chuva 2, sem chuva 8;

EC do pneu V: com chuva –6, sem chuva 7.

O coeficiente de rendimento climático (CRC) de um pneu é calculado como a soma dos produtos dos fatores de EC, com ou sem chuva, pelas correspondentes probabilidades de se ter tais condições climáticas: ele é utilizado para determinar qual pneu deve ser selecionado para uma dada corrida, escolhendo-se o pneu que apresentar o maior CRC naquele dia.

No dia de certa corrida, a probabilidade de chover era de 70% e o chefe da equipe calculou o CRC de cada um dos cinco tipos de pneu.

O pneu escolhido foi

1. I.
2. II.
3. III.
4. IV.
5. V.

15. (Enem Digital 2020) Uma casa lotérica oferece cinco opções de jogos. Em cada opção, o apostador escolhe um grupo de K números distintos em um cartão que contém um total Nde números disponíveis, gerando, dessa forma, um total de C combinações possíveis para se fazer a marcação do cartão. Ganha o prêmio o cartão que apresentar os K números sorteados. Os valores desses jogos variam de R$ 1,00 a R$ 2,00, conforme descrito no quadro.

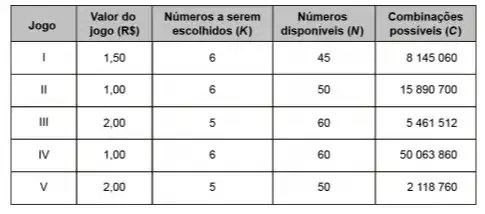
Um apostador dispõe de R$ 2,00 para gastar em uma das cinco opções de jogos disponíveis.

Segundo o valor disponível para ser gasto, o jogo que oferece ao apostador maior probabilidade de ganhar prêmio é o

1. I.
2. II.
3. III.
4. IV.
5. V.

16. (Enem Digital 2020) Um apostador deve escolher uma entre cinco moedas ao acaso e lançá-la sobre uma mesa, tentando acertar qual resultado (cara ou coroa) sairá na face superior da moeda.

Suponha que as cinco moedas que ele pode escolher sejam diferentes:

• duas delas têm “cara” nas duas faces;

• uma delas tem “coroa” nas duas faces;

• duas delas são normais (cara em uma face e coroa na outra).

Nesse jogo, qual é a probabilidade de o apostador obter uma face "cara" no lado superior da moeda lançada por ele?

1. $\frac{1}{8}$
2. $\frac{2}{5}$
3. $\frac{3}{5}$
4. $\frac{3}{4}$
5. $\frac{4}{5}$

17. (Enem PPL 2020) Para um docente estrangeiro trabalhar no Brasil, ele necessita validar o seu diploma junto ao Ministério da Educação. Num determinado ano, somente para estrangeiros que trabalharão em universidades dos estados de São Paulo e Rio de Janeiro, foram validados os diplomas de 402 docentes estrangeiros. Na tabela, está representada a distribuição desses docentes estrangeiros, por países de origem, para cada um dos dois estados.

A probabilidade de se escolher, aleatoriamente, um docente espanhol, sabendo-se que ele trabalha em uma universidade do estado de São Paulo é

1. 60/402
2. 60/239
3. 60/100
4. 100/239
5. 279/402

18. (Enem PPL 2020) Em uma campanha promocional de uma loja, um cliente gira uma roleta, conforme a apresentada no esquema, almejando obter um desconto sobre o valor total de sua compra. O resultado é o que está marcado na região apontada pela seta, sendo que todas as regiões são congruentes. Além disso, um dispositivo impede que a seta venha a apontar exatamente para a linha de fronteira entre duas regiões adjacentes. Um cliente realiza uma compra e gira a roleta, torcendo para obter o desconto máximo.

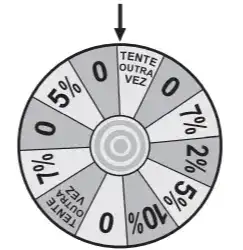
A probabilidade, em porcentagem, de esse cliente ganhar o desconto máximo com um único giro da roleta é melhor aproximada por

1. 8,3.
2. 10,0.
3. 12,5.
4. 16,6.
5. 50,0

19. (Enem PPL 2019) Uma locadora possui disponíveis 120 veículos da categoria que um cliente pretende locar. Desses, 20% são da cor branca, 40% são da cor cinza, 16 veículos são da cor vermelha e o restante, de outras cores. O cliente não gosta da cor vermelha e ficaria contente com qualquer outra cor, mas o sistema de controle disponibiliza os veículos sem levar em conta a escolha da cor pelo cliente.

Disponibilizando aleatoriamente, qual é a probabilidade de o cliente ficar contente com a cor do veículo?

1. $\frac{\mathrm{16}}{\mathrm{120}}$
2. $\frac{\mathrm{32}}{\mathrm{120}}$
3. $\frac{\mathrm{72}}{\mathrm{120}}$
4. $\frac{\mathrm{101}}{\mathrm{120}}$
5. $\frac{\mathrm{104}}{\mathrm{120}}$

20. (Enem PPL 2019) Uma empresa sorteia prêmios entre os funcionários como reconhecimento pelo tempo trabalhado. A tabela mostra a distribuição de frequência de 20 empregados dessa empresa que têm de 25 a 35 anos trabalhados. A empresa sorteou, entre esses empregados, uma viagem de uma semana, sendo dois deles escolhidos aleatoriamente.

Qual a probabilidade de que ambos os sorteados tenham 34 anos de trabalho?

1. $\frac{1}{\mathrm{20}}$
2. $\frac{1}{\mathrm{19}}$
3. $\frac{1}{\mathrm{16}}$
4. $\frac{2}{\mathrm{20}}$
5. $\frac{5}{\mathrm{20}}$

21. (Enem 2019) O dono de um restaurante situado às margens de uma rodovia percebeu que, ao colocar uma placa de propaganda de seu restaurante ao longo da rodovia, as vendas aumentaram. Pesquisou junto aos seus clientes e concluiu que a probabilidade de um motorista perceber uma placa de anúncio é $\frac{1}{2}$. Com isso, após autorização do órgão competente, decidiu instalar novas placas com anúncios de seu restaurante ao longo dessa rodovia, de maneira que a probabilidade de um motorista perceber pelo menos uma das placas instaladas fosse superior a $\frac{\mathrm{99}}{\mathrm{100}}$

A quantidade mínima de novas placas de propaganda a serem instaladas é

1. 99
2. 51
3. 50
4. 6
5. 1

22. (Enem 2019) Em um determinado ano, os computadores da receita federal de um país identificaram como inconsistentes 20% das declarações de imposto de renda que lhe foram encaminhadas. Uma declaração é classificada como inconsistente quando apresenta algum tipo de erro ou conflito nas informações prestadas. Essas declarações consideradas inconsistentes foram analisadas pelos auditores, que constataram que 25% delas eram fraudulentas. Constatou-se ainda que, dentre as declarações que não apresentaram inconsistências, 6,25% eram fraudulentas.

Qual é a probabilidade de, nesse ano, a declaração de um contribuinte ser considerada inconsistente, dado que ela era fraudulenta?

1. 0,0500
2. 0,1000
3. 0,1125
4. 0,3125
5. 0,5000

23. (Enem 2018) Para ganhar um prêmio, uma pessoa deverá retirar, sucessivamente e sem reposição, duas bolas pretas de uma mesma urna.

Inicialmente, as quantidades e cores das bolas são como descritas a seguir:

• Urna A – Possui três bolas brancas, duas bolas pretas e uma bola verde;

• Urna B – Possui seis bolas brancas, três bolas pretas e uma bola verde;

• Urna C – Possui duas bolas pretas e duas bolas verdes;

• Urna D – Possui três bolas brancas e três bolas pretas.

A pessoa deve escolher uma entre as cinco opções apresentadas:

• Opção 1 – Retirar, aleatoriamente, duas bolas da urna A;

• Opção 2 – Retirar, aleatoriamente, duas bolas da urna B;

• Opção 3 – Passar, aleatoriamente, uma bola da urna C para a urna A; após isso, retirar, aleatoriamente, duas bolas da urna A;

• Opção 4 – Passar, aleatoriamente, uma bola da urna D para a urna C; após isso, retirar, aleatoriamente, duas bolas da urna C;

• Opção 5 – Passar, aleatoriamente, uma bola da urna C para a urna D; após isso, retirar, aleatoriamente, duas bolas da urna D.

Com o objetivo de obter a maior probabilidade possível de ganhar o prêmio, a pessoa deve escolher a opção:

1. 1
2. 2
3. 3
4. 4
5. 5

24. (Enem 2018) Um designer de jogos planeja um jogo que faz uso de um tabuleiro de dimensão n x n, com n ≥ 2, no qual cada jogador, na sua vez, coloca uma peça sobre uma das casas vazias do tabuleiro.

Quando uma peça é posicionada, a região formada pelas casas que estão na mesma linha ou coluna dessa peça é chamada de zona de combate dessa peça. Na figura está ilustrada a zona de combate de uma peça colocada em uma das casas de um tabuleiro de dimensão 8 x 8.

O tabuleiro deve ser dimensionado de forma que a probabilidade de se posicionar a segunda peça aleatoriamente, seguindo a regra do jogo, e esta ficar sobre a zona de combate da primeira, seja inferior a $\frac{1}{5}$ .

A dimensão mínima que o designer deve adotar para esse tabuleiro é:

1. 4 x 4.
2. 6 x 6.
3. 9 x 9.
4. 10 x 10.
5. 11 x 11.

25. (Enem 2018) Um rapaz estuda em uma escola que fica longe de sua casa, e por isso precisa utilizar o transporte público. Como é muito observador, todos os dias ele anota a hora exata (sem considerar os segundos) em que o ônibus passa pelo ponto de espera.

Também notou que nunca consegue chegar ao ponto de ônibus antes de 6h 15min da manhã. Analisando os dados coletados durante o mês de fevereiro, o qual teve 21 dias letivos, ele concluiu que 6h 21min foi o que mais se repetiu, e que a mediana do conjunto de dados é 6h 22min.

A probabilidade de que, em algum dos dias letivos de fevereiro, esse rapaz tenha apanhado o ônibus antes de 6h 21min da manhã é, no máximo,

1. $\frac{4}{\mathrm{21}}$
2. $\frac{5}{\mathrm{21}}$
3. $\frac{6}{\mathrm{21}}$
4. $\frac{7}{\mathrm{21}}$
5. $\frac{8}{\mathrm{21}}$

26. (Enem 2018) O salto ornamental é um esporte em que cada competidor realiza seis saltos. A nota em cada salto é calculada pela soma das notas dos juízes, multiplicada pela nota de partida (o grau de dificuldade de cada salto). Fica em primeiro lugar o atleta que obtiver a maior soma das seis notas recebidas.

O atleta 10 irá realizar o último salto da final. Ele observa no Quadro 1, antes de executar o salto, o recorte do quadro parcial de notas com a sua classificação e a dos três primeiros lugares até aquele momento.

Ele precisa decidir com seu treinador qual salto deverá realizar. Os dados dos possíveis tipos de salto estão no Quadro 2.

O atleta optará pelo salto com a maior probabilidade de obter a nota estimada, de maneira que lhe permita alcançar o primeiro lugar.

1. T1
2. T2
3. T3
4. T4
5. T5

27. (Enem 2017) Numa avenida existem 10 semáforos. Por causa de uma pane no sistema, os semáforos ficaram sem controle durante uma hora, e fixaram suas luzes unicamente em verde ou vermelho. Os semáforos funcionam de forma independente; a probabilidade de acusar a cor verde é de $\frac{2}{3}$ e a de acusar a cor vermelha é de $\frac{1}{3}$ Uma pessoa percorreu a pé toda essa avenida durante o período da pane, observando a cor da luz de cada um desses semáforos.

Qual a probabilidade de que esta pessoa tenha observado exatamente um sinal na cor verde?

1. $\frac{10{\times }_2}{3^{10}}$
2. $\frac{10\times \; <!--\; multiplication\; sign\; -->2^9}{3^{10}}$
3. $\frac{10\times \; <!--\; multiplication\; sign\; -->2^9}{3^{10}}$
4. $\frac{2^{90}}{3^{100}}$
5. $\frac{2}{3^{10}}$