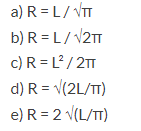Círculos e Circunferência
Lista de 21 exercícios de Matemática com gabarito sobre o tema Círculos e Circunferência com questões do Enem.
Você pode conferir as videoaulas, conteúdo de teoria, e mais questões sobre o tema Círculos e Circunferência.
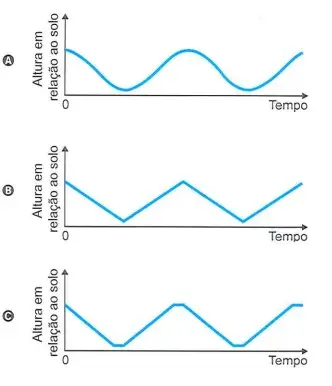
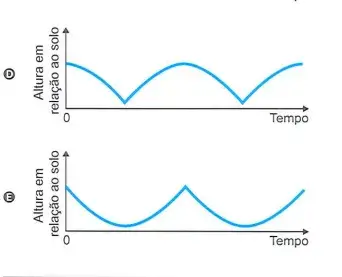
01. (Enem 2023) A figura ilustra uma roda-gigante no exato instante em que a cadeira onde se encontra a pessoa P está no ponto mais alto dessa roda-gigante.
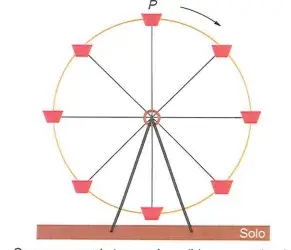
Com o passar do tempo, à medida que a roda-gigante gira, com velocidade angular constante e no sentido horário, a altura da cadeira onde se encontra a pessoa P, em relação ao solo, vai se alterando.
O gráfico que melhor representa a variação dessa altura, em função do tempo, contado a partir do instante em que a cadeira da pessoa P se encontra na posição mais alta da roda-gigante, é
02. (Enem 2023) Num certo momento de um jogo digital, a tela apresenta a imagem representada na figura. O ponto Q1 representa a posição de um jogador que está com a bola, os pontos Q2, Q3, Q4, Q5 e Q6 também indicam posições de jogadores da mesma equipe, e os pontos A e B indicam os dois pés da trave mais próxima deles. No momento da partida retratado, o jogador Q1 tem a posse da bola, que será passada para um dos outros jogadores das posições Qn, n ∈ {2, 3, 4, 5, 6}, cujo ângulo AQnB tenha a mesma medida do ângulo α = AQ1B.
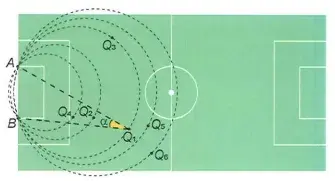
Qual é o jogador que receberá a bola?
- Q2
- Q3
- Q4
- Q5
- Q6
03. (Enem 2023) As figuras pintadas no quadro da sala de estar de uma residência representam as silhuetas de parte das torres de um castelo e, ao fundo, a de uma lua cheia. A lua foi pintada na forma de um círculo, e o telhado da torre mais alta, na forma de triângulo equilátero, foi pintado sobrepondo parte da lua. O centro da lua coincide com um dos vértices do telhado da torre mais alta.
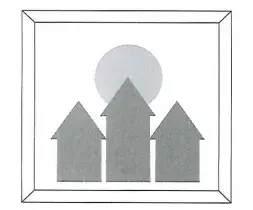
Nesse quadro, a parte da lua escondida atrás da torre mais alta do castelo pode ser representada por um
- cone.
- setor circular.
- segmento circular.
- triângulo isósceles.
- arco de circunferência.
04. (ENEM PPL 2022) Uma empresa de publicidade está criando um logotipo que tem o formato indicado na figura. O círculo menor está inscrito no quadrado ABCD, e o círculo maior circunscreve o mesmo quadrado. Considere S1 a área do círculo menor e S2 a área do círculo maior
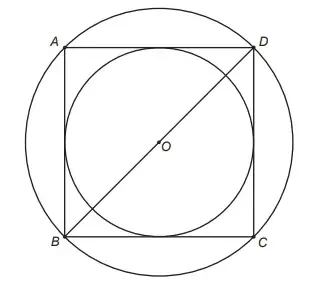
A razão da área do círculo maior para o círculo menor é igual a
- √2
- 1/2
- 2
- 8
- 16
05. (ENEM PPL 2022) Um cortador de grama elétrico tem o cabo plugado em uma tomada fixa rente ao solo plano de um gramado. O cabo de energia mede 5 metros, e o cortador tem uma lâmina que corta 1 metro de largura. Atualmente ele corta, portanto, uma região no formato de círculo de raio 6 m, como ilustra a figura. Pretende-se usar adicionalmente um cabo extensor, de modo que seja possível cortar uma região com o dobro da área que corta atualmente.
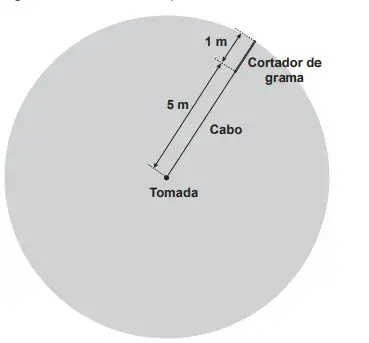
Qual a medida aproximada, em metro, do comprimento do cabo extensor?
- 12,0
- 8,5
- 6,0
- 3,0
- 2,5
06. (Enem PPL 2020) Um vidraceiro precisa construir tampos de vidro com formatos diferentes, porém com medidas de áreas iguais. Para isso, pede a um amigo que o ajude a determinar uma fórmula para o cálculo do raio R de um tampo de vidro circular com área equivalente à de um tampo de vidro quadrado de lado L
A fórmula correta é
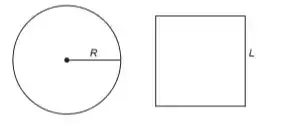
07. (Enem PPL 2020) Dois atletas partem de pontos, respectivamente P1 e P2 , em duas pistas planas distintas, conforme a figura, deslocando-se no sentido anti-horário até a linha de chegada, percorrendo, desta forma, a mesma distância (L). Os trechos retos dos finais das curvas até a linha de chegada desse percurso têm o mesmo comprimento (l) nas duas pistas e são tangentes aos trechos curvos, que são semicírculos de centro C. O raio do semicírculo maior é R1 e o raio do semicírculo menor é R2.
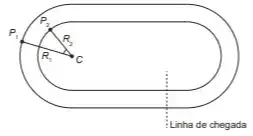
Sabe-se que o comprimento de um arco circular é dado pelo produto do seu raio pelo ângulo, medido em radiano, subentendido pelo arco. Nas condições apresentadas, a razão da medida do ângulo P2CP1 pela diferença L− I é dada por

08. (Enem PPL 2019) O dono de um salão de festas precisa decorar cinco pilastras verticais cilíndricas idênticas, cujo raio da base mede 10 cm. O objetivo é revestir integralmente essas pilastras com faixas de menor comprimento possível, de modo que cada uma tenha seis faixas de cor preta e cinco faixas de cor branca, conforme ilustrado na figura.

Ele orçou as faixas em cinco lojas que as comercializam na largura e nas cores desejadas, porém, em todas elas, só são vendidas peças inteiras. Os comprimentos e os respectivos preços das peças comercializadas por loja estão apresentados no quadro. 
O dono do salão de festas decidiu efetuar a compra em uma única loja, optando por aquela em que a compra ficaria mais barata.
Utilize 3 como valor aproximado para π.
A loja na qual o dono do salão de festas deve comprar as peças necessárias para confeccionar as faixas é
- I
- II.
- III.
- IV.
- V.
09. (Enem PPL 2019) Uma pista circular delimitada por duas circunferências concêntricas foi construída. Na circunferência interna dessa pista, de raio 0,3 km, serão colocados aparelhos de ginástica localizados nos pontos P, Q e R, conforme a figura.

O segmento RP é um diâmetro dessa circunferência interna, e o ângulo P Q tem medida igual a radianos.
Para uma pessoa ir do ponto P ao ponto Q andando pela circunferência interna no sentido anti-horário, ela percorrerá uma distância, em quilômetro, igual a
- 0,009π
- 0,03π
- 0,06π
- 0,12π
- 0,18π
10. (Enem 2019) Em um condomínio, uma área pavimentada, que tem a forma de um círculo com diâmetro medindo 6 m, é cercada por grama. A administração do condomínio deseja ampliar essa área, mantendo seu formato circular, e aumentando, em 8 m, o diâmetro dessa região, mantendo o revestimento da parte já existente. O condomínio dispõe, em estoque, de material suficiente para pavimentar mais 100 m² de área.
O síndico do condomínio irá avaliar se esse material disponível será suficiente para pavimentar a região a ser ampliada.
Utilize 3 como aproximação para π.
A conclusão correta a que o síndico deverá chegar, considerando a nova área a ser pavimentada, é a de que o material disponível em estoque
- será suficiente, pois a área da nova região a ser pavimentada mede 21 m².
- será suficiente, pois a área da nova região a ser pavimentada mede 24 m².
- será suficiente, pois a área da nova região a ser pavimentada mede 48 m².
- não será suficiente, pois a área da nova região a ser pavimentada mede 108 m².
- não será suficiente, pois a área da nova região a ser pavimentada mede 120 m².
11. (Enem 2019) Um ciclista quer montar um sistema de marchas usando dois discos dentados na parte traseira de sua bicicleta, chamados catracas. A coroa é o disco dentado que é movimentado pelos pedais da bicicleta, sendo que a corrente transmite esse movimento às catracas, que ficam posicionadas na roda traseira da bicicleta.
As diferentes marchas ficam definidas pelos diferentes diâmetros das catracas, que são medidos conforme indicação na figura.

O ciclista já dispõe de uma catraca com 7 cm de diâmetro e pretende incluir uma segunda catraca, de modo que, à medida em que a corrente passe por ela, a bicicleta avance 50% a mais do que avançaria se a corrente passasse pela primeira catraca, a cada volta completa dos pedais.
O valor mais próximo da medida do diâmetro da segunda catraca, em centímetro e com uma casa decimal, é
- 2,3
- 3,5
- 4,7
- 5,3
- 10,5
12. (Enem 2018) Sobre um sistema cartesiano considera-se uma malha formada por circunferências de raios com medidas dadas por números naturais e por 12 semirretas com extremidades na origem, separadas por ângulos de.
conforme a figura.

Suponha que os objetos se desloquem apenas pelas semirretas e pelas circunferências dessa malha, não podendo passar pela origem (0;0).
Considere o valor de π com aproximação de, pelo menos, uma casa decimal.
Para realizar o percurso mais curto possível ao longo da malha, do ponto B até o ponto A, um objeto deve percorrer uma distância igual a:
13. (Enem 2017) A manchete demonstra que o transporte de grandes cargas representa cada vez mais preocupação quando feito em vias urbanas.
Caminhão entala em viaduto no Centro
Um caminhão de grande porte entalou embaixo do viaduto no cruzamento das avenidas Borges de Medeiros e Loureiro da Silva no sentido Centro-Bairro, próximo à Ponte de Pedra, na capital. Esse veículo vinha de São Paulo para Porto Alegre e transportava três grandes tubos, conforme ilustrado na foto.

Considere que o raio externo de cada cano da imagem seja 0,60 m e que eles estejam em cima de uma carroceria cuja parte superior está a 1,30 m do solo. O desenho representa a vista traseira do empilhamento dos canos.

A margem de segurança recomendada para que um veículo passe sob um viaduto é que a altura total do veículo com a carga seja, no mínimo, 0,50 m menor do que a altura do vão do viaduto.
Considere 1,7 como aproximação para
Qual deveria ser a altura mínima do viaduto, em metro, para que esse caminhão pudesse passar com segurança sob seu vão?
- 2,82.
- 3,52.
- 3,70.
- 4,02.
- 4,20.
14. (Enem 2017) Uma pessoa ganhou uma pulseira formada por pérolas esféricas, na qual faltava uma das pérolas. A figura indica a posição em que estaria faltando esta pérola.

Ela levou a jóia a um joalheiro que verificou que a medida do diâmetro dessas pérolas era 4 milímetros. Em seu estoque, as pérolas do mesmo tipo e formato, disponíveis para reposição, tinham diâmetros iguais a: 4,025 mm; 4,100 mm; 3,970 mm; 4,080 mm e 3,099 mm.
O joalheiro então colocou na pulseira a pérola cujo diâmetro era o mais próximo do diâmetro das pérolas originais.
A pérola colocada na pulseira pelo joalheiro tem diâmetro, em milímetro, igual a
- 3,099.
- 3,970.
- 4,025.
- 4,080.
- 4,100.
15. (Enem 2017) Pivô central é um sistema de irrigação muito usado na agricultura, em que uma área circular é projetada para receber uma estrutura suspensa. No centro dessa área, há uma tubulação vertical que transmite água através de um cano horizontal longo, apoiado em torres de sustentação, as quais giram, sobre rodas, em torno do centro do pivô, também chamado de base, conforme mostram as figuras. Cada torre move-se com velocidade constante.

Um pivô de três torres (T1, T2 e T3) será instalado em uma fazenda, sendo que as distâncias entre torres consecutivas bem como da base à torre T1 são iguais a 50 m. O fazendeiro pretende ajustar as velocidades das torres, de tal forma que o pivô efetue uma volta completa em 25 horas. Use 3 como aproximação para π.
Para atingir seu objetivo, as velocidades das torres T1, T2 e T3 devem ser, em metro por hora, de
- 12, 24 e 36.
- 6, 12 e 18.
- 2, 4 e 6.
- 300, 1200 e 2700.
- 600, 2400 e 5400.
16. (Enem 2016) A London Eye é uma enorme roda-gigante na capital inglesa. Por ser um dos monumentos construídos para celebrar a entrada do terceiro milênio, ela também é conhecida como Roda do Milênio. Um turista brasileiro, em visita à Inglaterra, perguntou a um londrino o diâmetro (destacado na imagem) da Roda do Milênio e ele respondeu que ele tem 443 pés.

Não habituado com a unidade pé, e querendo satisfazer sua curiosidade, esse turista consultou um manual de unidades de medidas e constatou que 1 pé equivale a 12 polegadas, e que 1 polegada equivale a 2,54 cm. Após alguns cálculos de conversão, o turista ficou surpreendido com o resultado obtido em metros.
Qual a medida que mais se aproxima do diâmetro da Roda do Milênio, em metro?
- 53
- 94
- 113
- 135
- 145
17. (Enem 2016) Em uma cidade será construída uma galeria subterrânea que receberá uma rede de canos para o transporte de água de uma fonte (F) até o reservatório de um novo bairro (B). Após avaliações, foram apresentados dois projetos para o trajeto de construção da galeria: um segmento de reta que atravessaria outros bairros ou uma semicircunferência que contornaria esses bairros, conforme ilustrado no sistema de coordenadas xOy da figura, em que a unidade de medida nos eixos é o quilômetro.

Estudos de viabilidade técnica mostraram que, pelas características do solo, a construção de 1 m de galeria via segmento de reta demora 1,0 h, enquanto que 1 m de construção de galeria via semicircunferência demora 0,6 h. Há urgência em disponibilizar água para esse bairro.
Use 3 como aproximação para π e 1,4 como aproximação para √2.
O menor tempo possível, em hora, para conclusão da construção da galeria, para atender às necessidades de água do bairro, é de
- 1 260.
- 2 520.
- 2 800.
- 3 600.
- 4 000.
18. (Enem 2016) Um marceneiro está construindo um material didático que corresponde ao encaixe de peças de madeira com 10 cm de altura e formas geométricas variadas, num bloco de madeira em que cada peça se posicione na perfuração com seu formato correspondente, conforme ilustra a figura. O bloco de madeira já possui três perfurações prontas de bases distintas: uma quadrada (Q), de lado 4 cm, uma retangular (R), com base 3 cm e altura 4 cm, e uma em forma de um triângulo equilátero (T), de lado 6,8 cm. Falta realizar uma perfuração de base circular (C).
O marceneiro não quer que as outras peças caibam na perfuração circular e nem que a peça de base circular caiba nas demais perfurações e, para isso, escolherá o diâmetro do círculo que atenda a tais condições. Procurou em suas ferramentas uma serra copo (broca com formato circular) para perfurar a base em madeira, encontrando cinco exemplares, com diferentes medidas de diâmetros, como segue: (I) 3,8 cm; (II) 4,7 cm; (III) 5,6 cm; (IV) 7,2 cm e (V) 9,4 cm.

Considere 1,4 e 1,7 como aproximações para √2 e √3, respectivamente
Para que seja atingido o seu objetivo, qual dos exemplares de serra copo o marceneiro deverá escolher?
- I
- II
- III
- IV
- V
19. (Enem PPL 2015) No jogo mostrado na figura, uma bolinha descola-se somente de duas formas: ao longo de linhas retas ou por arcos de circunferências centradas no ponto O e raios variando de 1 a 8. Durante o jogo, a bolinha que estiver no ponto P deverá realizar a seguinte sequência de movimentos: 2 unidades no mesmo sentido utilizado para ir do ponto O até o ponto A e, no sentido anti-horário, um arco de circunferência cujo ângulo central é 120°.

Após a sequência de movimentos descrita, a bolinha estará no ponto
- B
- D
- E
- F
- G
20. (Enem PPL 2015) A figura é uma representação simplificada do carrossel de um parque de diversões, visto de cima. Nessa representação, os cavalos estão identificados pelos pontos escuros, e ocupam circunferências de raios 3 m e 4 m, respectivamente, ambas centradas no ponto O. Em cada sessão de funcionamento, o carrossel efetua 10 voltas.

Quantos metros uma criança sentada no cavalo C1 percorrerá a mais do que uma criança no cavalo C2 , em uma sessão? Use 3,0 como aproximação para S.
- 55,5
- 60,0
- 175,5
- 235,5
- 240,0
21. (Enem 2016) De forma geral, os pneus radiais trazem em sua lateral uma marcação do tipo abc/deRfg, como 185/65R15. Essa marcação identifica as medidas do pneu da seguinte forma:
• abc é a medida da largura do pneu, em milímetro;
• de é igual ao produto de 100 pela razão entre a medida da altura (em milímetro) e a medida da largura do pneu (em milímetro);
• R significa radial;
• fg é a medida do diâmetro interno do pneu, em polegada.
A figura ilustra as variáveis relacionadas com esses dados.

O proprietário de um veículo precisa trocar os pneus de seu carro e, ao chegar a uma loja, é informado por um vendedor que há somente pneus com os seguintes códigos: 175/65R15, 175/75R15, 175/80R15, 185/60R15 e 205/55R15. Analisando, juntamente com o vendedor, as opções de pneus disponíveis, concluem que o pneu mais adequado para seu veículo é o que tem a menor altura.
Desta forma, o proprietário do veículo deverá comprar o pneu com a marcação
- 205/55R15.
- 175/65R15.
- 175/75R15.
- 175/80R15.
- 185/60R15