Matriz e Sistema Linear

01. (ENEM 2021) Uma pessoa pretende viajar por uma companhia aérea que despacha gratuitamente uma mala com até 10 kg.

Em duas viagens que realizou, essa pessoa utilizou a mesma mala e conseguiu 10 kg com as seguintes combinações de itens:

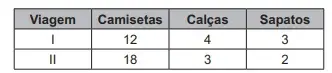
Para ter certeza de que sua bagagem terá massa de 10 kg, ela decide levar essa mala com duas calças, um sapato e o máximo de camisetas, admitindo que itens do mesmo tipo têm a mesma massa.

Qual a quantidade máxima de camisetas que essa pessoa poderá levar?

1. 22
2. 24
3. 26
4. 33
5. 39

02. (ENEM PPL 2022) Uma faculdade oferece dois cursos diferentes na área de Humanas. Para um aluno ingressar nesses cursos, o vestibular contém questões objetivas e uma redação, e a nota final do candidato é a soma dessas notas, utilizando o seguinte critério de pesos:

• questões objetivas: peso 1 para o curso I e peso 1 para o curso II;

• redação: peso 2 para o curso I e peso 3 para o curso II.

Um candidato que concorre aos dois cursos obteve nota X nas questões objetivas e nota Y na redação. Para analisar sua nota para o curso I e para o curso II, o candidato representa sua nota com um produto de matrizes A . B, em que a matriz A representa os pesos, e a matriz B contém as notas obtidas pelo candidato. A matriz resultante A . B é uma matriz coluna, em que, na primeira linha, tem sua nota final para o curso I e, na segunda linha, tem sua nota final para o curso II.

Nessas condições, qual representação algébrica gera o resultado final desse candidato nos dois cursos?

03. (ENEM PPL 2022) Três amigos, A, B e C, se encontraram em um supermercado. Por coincidência, estavam comprando os mesmos itens, conforme o quadro.

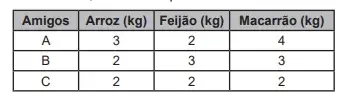
Os amigos estavam muito entretidos na conversa e nem perceberam que pagaram suas compras, pegaram seus trocos e esqueceram seus comprovantes. Já longe do supermercado, “A” lembrou que precisava saber o quanto pagou por um quilo de arroz e dois quilos de macarrão, pois estava comprando para sua vizinha e esperava ser ressarcido. “B”, que adorava desafios matemáticos, disse que pagou suas compras com R$ 40,00 e obteve troco de R$ 7,30, e que conseguiria determinar o custo desses itens se os amigos dissessem como pagaram e quanto foram seus respectivos trocos. “A” disse que pagou com R$ 40,00 e obteve troco de R$ 4,00, e “C” pagou com R$ 30,00 e obteve troco de R$ 5,40.

A vizinha de “A” deve a ele pela compra, em reais, o valor de

1. 8,10.
2. 10,00.
3. 11,40.
4. 12,00.
5. 13,20.

04. (ENEM 2021) Uma construtora, pretendendo investir na construção de imóveis em uma metrópole com cinco grandes regiões, fez uma pesquisa sobre a quantidade de famílias que mudaram de uma região para outra, de modo a determinar qual região foi o destino do maior fluxo de famílias, sem levar em consideração o número de famílias que deixaram a região. Os valores da pesquisa estão dispostos em uma matriz A = [aij], i, j ∈ {1,2,3,4,5}, em que o elemento aij corresponde ao total de famílias (em dezena) que se mudaram da região i para a região j durante um certo período, e o elemento aij é considerado nulo, uma vez que somente são consideradas mudanças entre regiões distintas. A seguir, está apresentada a matriz com os dados da pesquisa.

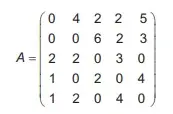
Qual região foi selecionada para o investimento da construtora?

1. 1
2. 2
3. 3
4. 4
5. 5

05. (Enem 2020) Uma empresa avaliou os cinco aparelhos de celulares (T₁, T₂, T₃, T₄ e T₅) mais vendidos no último ano, nos itens: câmera, custo-benefí cio, design, desempenho da bateria e tela, representados por I₁, I₂, I₃, I₄ e I₅, respectivamente. A empresa atribuiu notas de 0 a 10 para cada item avaliado e organizou essas notas em uma matriz A, em que cada elemento a_ij significa a nota dada pela empresa ao aparelho T_i no item I_j. A empresa considera que o melhor aparelho de celular é aquele que obtém a maior soma das notas obtidas nos cinco itens avaliados.

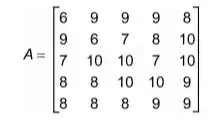
Com base nessas informações, o aparelho de celular que a empresa avaliou como sendo o melhor é o

1. T1.
2. T2.
3. T3.
4. T4.
5. T5

06. (Enem 2019) Um professor aplica, durante os cinco dias úteis de uma semana, testes com quatro questões de múltipla escolha a cinco alunos. Os resultados foram representados na matriz.

Nessa matriz os elementos das linhas de 1 a 5 representam as quantidades de questões acertadas pelos alunos Ana, Bruno, Carlos, Denis e Érica, respectivamente, enquanto que as colunas de 1 a 5 indicam os dias da semana, de segunda-feira a sexta-feira, respectivamente, em que os testes foram aplicados.

O teste que apresentou maior quantidade de acertos foi o aplicado na

1. segunda-feira.
2. terça-feira.
3. quarta-feira.
4. quinta-feira.
5. sexta-feira.

07. (Enem 2018) A Transferência Eletrônica Disponível (TED) é uma transação financeira de valores entre diferentes bancos. Um economista decide analisar os valores enviados por meio de TEDs entre cinco bancos (1, 2, 3, 4 e 5) durante um mês. Para isso, ele dispõe esses valores em uma matriz A = [a_ij], em que 1 ≤ i ≤ 5 e 1 ≤ j ≤ 5, e o elemento a_ij corresponde ao total proveniente das operações feitas via TED, em milhão de real, transferidos do banco i para o banco j durante o mês. Observe que os elementos aij = 0, uma vez que TED é uma transferência entre bancos distintos. Esta é a matriz obtida para essa análise:

Com base nessas informações, o banco que transferiu a maior quantia via TED é o banco:

1. 1
2. 2
3. 3
4. 4
5. 5

08. (Enem 2012) Um aluno registrou as notas bimestrais de algumas de suas disciplinas numa tabela. Ele observou que as entradas numéricas da tabela formavam uma matriz 4 × 4, e que poderia calcular as médias anuais dessas disciplinas usando produto de matrizes. Todas as provas possuı́am o mesmo peso, e a tabela que ele conseguiu é mostrada a seguir

Para obter essas médias, ele multiplicou a matriz obtida a partir da tabela por