Estática

Lista de 10 exercícios de Física com gabarito sobre o tema Estática com questões de Vestibulares.


Você pode conferir as videoaulas, conteúdo de teoria, e mais questões sobre o tema aqui.




1. (UNESP) Um Iustre está pendurado no teto de uma sala por meio de dois fios inextensíveis, de mesmo comprimento e de massas desprezíveis, como mostra a figura 1, onde o ângulo que cada fio faz com a vertical é 30°. As forças de tensão nos fios têm a mesma intensidade.

Um Iustre está pendurado no teto de uma sala por meio de dois fios inextensíveis, de mesmo comprimento e de massas desprezíveis, como mostra a figura 1, onde o ângulo que cada fio faz com a vertical é 30°.

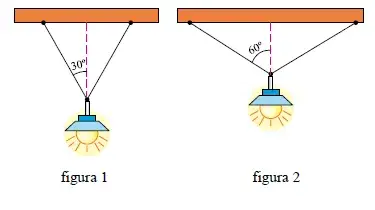
Considerando cos 30° ≅ 0,87, se a posição do Iustre for modificada e os fios forem presos ao teto mais distantes um do outro, de forma que o ângulo que cada um faz com a vertical passe a ser o dobro do original, como mostra a figura 2, a tensão em da fio será igual a

  1. 0,50 do valor original.
  2. 1 ,74 do valor original.
  3. 0,86 do valor original.
  4. 2,00 do valor original.
  5. 3,46 do valor original.

Resposta: B

Resolução:

2. (UERJ-RJ) Para abrir uma porta, você aplica sobre a maçaneta, colocada a uma distância d da dobradiça, conforme a figura abaixo, uma força de módulo F perpendicular à porta.

Para obter o mesmo efeito, o módulo da força que você deve aplicar em uma maçaneta colocada a uma distância d/2 da dobradiça desta mesma porta, é:

  1. F/2
  2. F
  3. 2F
  4. 4F
  5. 5F/2

Resposta: C

Resolução:

Para abrir uma porta, é necessário aplicar um momento de força suficiente para superar o momento de força gerado pelo peso da porta. O momento de força é dado pelo produto da força aplicada pela distância da força ao eixo de rotação.

No caso da primeira situação, a força é aplicada a uma distância d da dobradiça, que é o eixo de rotação. Portanto, o momento de força é dado por:

M1 = F * d

Para obter o mesmo efeito na segunda situação, o momento de força deve ser o mesmo. No entanto, a distância da força ao eixo de rotação é agora d/2. Portanto, a força necessária deve ser o dobro da força aplicada na primeira situação:

M2 = F' * d/2

M1 = M2

F * d = F' * d/2

F' = 2F

Portanto, a resposta correta é (C), 2F.

Explicação detalhada

O momento de força é uma grandeza física que mede a tendência de uma força em causar rotação. É dado pelo produto da força aplicada pela distância da força ao eixo de rotação.

No caso da porta, o eixo de rotação é a dobradiça. Para abrir a porta, é necessário aplicar um momento de força suficiente para superar o momento de força gerado pelo peso da porta.

No primeiro caso, a força é aplicada a uma distância d da dobradiça. Portanto, o momento de força é dado por:

M1 = F * d

No segundo caso, a distância da força ao eixo de rotação é agora d/2. Portanto, a força necessária deve ser o dobro da força aplicada na primeira situação para que o momento de força seja o mesmo:

M2 = F' * d/2

F * d = F' * d/2

F' = 2F

3. (CFT-CE) Três forças coplanares atuam sobre os cantos A, B e C de uma chapa quadrada, de peso desprezível, como mostra a figura. As forças têm módulos F1 = F2 = F e F3 = 2F.

Três forças coplanares atuam sobre os cantos A, B e C de uma chapa quadrada, de peso desprezível, como mostra a figura.

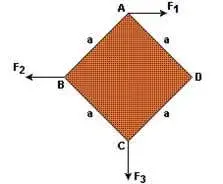
Deve-se aplicar uma quarta força F4 ao ponto D, de tal modo que evite a rotação da chapa em torno do seu centro. A intensidade dessa força e a sua direção valem, respectivamente,

  1. F, para direita.
  2. 2F, para cima.
  3. 2F, para esquerda.
  4. F, para cima.
  5. 2F, ao longo de um dos lados da chapa.

Resposta: D

Resolução:

Para que a chapa não gire em torno do seu centro, a quarta força F4 deve gerar um momento de força igual e oposto ao momento de força gerado pelas três primeiras forças.

O momento de força é dado pelo produto da força aplicada pelo braço de alavanca. No caso das três primeiras forças, o braço de alavanca é a distância entre o ponto de aplicação da força e o centro da chapa.

As três primeiras forças geram um momento de força no sentido horário. Portanto, a quarta força F4 deve gerar um momento de força no sentido anti-horário.

Para que o momento de força seja igual, a quarta força F4 deve ter o mesmo módulo das três primeiras forças, mas o braço de alavanca deve ser o dobro.

Portanto, a intensidade da quarta força F4 é de 2F e a sua direção é para esquerda.

Explicação detalhada

Para que a chapa não gire em torno do seu centro, a quarta força F4 deve gerar um momento de força igual e oposto ao momento de força gerado pelas três primeiras forças.

O momento de força é dado pelo produto da força aplicada pelo braço de alavanca. No caso das três primeiras forças, o braço de alavanca é a distância entre o ponto de aplicação da força e o centro da chapa.

As três primeiras forças geram um momento de força no sentido horário. Portanto, a quarta força F4 deve gerar um momento de força no sentido anti-horário.

Para que o momento de força seja igual, a quarta força F4 deve ter o mesmo módulo das três primeiras forças, mas o braço de alavanca deve ser o dobro.

Portanto, a intensidade da quarta força F4 é de 2F e a sua direção é para esquerda.

M1 = M2

F1 * d1 = F4 * d2

(F * d) = (2F * 2d)

F4 = 2F

d2 = d

4. (UNIFESP-SP) A figura representa um cilindro de massa m, que rola para a direita sobre uma prancha homogênea e horizontal de massa 2m, assentada livremente em dois apoios verticais, sobre os quais não desliza.

Pode-se afirmar que a prancha começa a tombar quando o cilindro passa pelo ponto

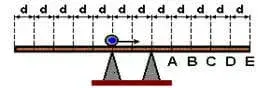
A figura representa um cilindro de massa m, que rola para a direita sobre uma prancha homogênea e horizontal de massa 2m, assentada livremente em dois apoios verticais, sobre os quais não desliza.
  1. A
  2. B
  3. C
  4. D
  5. E

Resposta: B

Resolução:

5. (PUC-PR) A barra AB, homogênea de peso P, pode girar em torno da articulação em C. Ela é mantida em equilíbrio pelos corpos D e E de massas e volumes diferentes. O corpo E está totalmente imerso na água, figura 1.

A barra AB, homogênea de peso P, pode girar em torno da articulação em C. Ela é mantida em equilíbrio pelos corpos D e E de massas e volumes diferentes. O corpo E está totalmente imerso na água, figura 1.

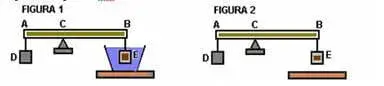
Considere as proposições.

I. Se a barra está em equilibrio, podemos afirmar que o momento das forças atuantes sobre a barra em relação ao ponto C é nulo.

II. Se o corpo E for retirado da água, figura 2, o equilíbrio será desfeito, e a barra girará em torno de C, no sentido horário.

III. Se o corpo E for retirado da água, figura 2, o equilíbrio será desfeito, e a barra girará em torno de C, no sentido anti-horário.

IV. Se o corpo E for retirado da água, figura 2, não será alterado o equilíbrio da barra.

Está correta ou estão corretas:

  1. Somente I.
  2. Somente II .
  3. I e III.
  4. I e II .
  5. Somente IV.

Resposta: D

Resolução:

6. (FUVEST-SP) Um avião, com massa M = 90 toneladas, para que esteja em equilíbrio em vôo, deve manter seu centro de gravidade sobre a linha vertical CG, que dista 16m do eixo da roda dianteira e 4,0m do eixo das rodas traseiras, como na figura abaixo. Para estudar a distribuição de massas do avião, em solo, três balanças são colocadas sob as rodas do trem de aterrissagem. A balança sob a roda dianteira indica ND e cada uma das que estão sob as rodas traseiras indica NT.

Um avião, com massa M = 90 toneladas, para que esteja em equilíbrio em vôo, deve manter seu centro de gravidade sobre a linha vertical CG, que dista 16m do eixo da roda dianteira e 4,0m do eixo das rodas traseiras, como na figura abaixo.

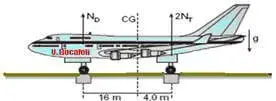
Uma distribuição de massas, compatível com o equilíbrio do avião em vôo, poderia resultar em indicações das balanças, em toneladas, correspondendo aproximadamente a:

  1. ND = 0 NT = 45
  2. ND = 10 NT = 40
  3. ND = 18 NT = 36
  4. ND = 30 NT = 30
  5. ND = 72 NT = 9,0

Resposta: C

Resolução:

7. (UEL-PR) Uma tesoura é uma ferramenta construída para ampliar a força exercida pela mão que a utiliza para cortar objetos.

Uma tesoura é uma ferramenta construída para ampliar a força exercida pela mão que a utiliza para cortar objetos.

A essa ampliação da força dá-se o nome de “vantagem mecânica”, dada por F2/F1=d1/d2, onde o índice 1 é relativo ao cabo, e o índice 2 está relacionado à lâmina de corte. Sobre a vantagem mecânica da tesoura, é correto afirmar:

  1. Se d1 for menor que d2, F2 é maior que F1
  2. Se d1 for menor que d2, F2 é igual a F1
  3. Se d1 for maior que d2, F2 é maior que F1
  4. Se d1 for menor que d2, F2 é menor que F1
  5. Se d1 for igual a d2, F2 é menor que F1

Resposta: C

Resolução:

Se d1 for maior que d2, F2 é maior que F1

8. (CFT-MG) No desenho abaixo, um corpo B, de massa igual a 4M, está suspenso em um dos pontos equidistantes de uma barra homogênea, de comprimento L e massa M, que se encontra apoiado em uma cunha.

No desenho abaixo, um corpo B, de massa igual a 4M, está suspenso em um dos pontos equidistantes de uma barra homogênea, de comprimento L e massa M, que se encontra apoiado em uma cunha.
  1. I
  2. II
  3. III
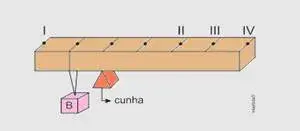
  4. IV

Resposta: C

Resolução:

Para que o corpo esteja em equilíbrio, a resultante dos momentos das forças que atuam no sistema em relação ao ponto de apoio deve ser zero.

Considerando o comprimento total da barra como x, o peso da barra atua no seu centro de massa que fica x/6 a direita do ponto de apoio. Assim teremos -

MPb - (Mb + MPa) = 0

MPb = Mb + MPa

O momento de uma força é calculado pelo produto da força pela distância ao ponto de apoio.

M = F·d

(4M·g)·x/6 = M·g·x/6 + M·g·d

(4M·g)·x/6 - M·g·x/6 = Mgd (divide tudo por Mg)

4x/6 - x/6 = d

3x/6 = d

x/3 = d (à direita do ponto de apoio)

9. (FGV-RJ) Três adolescentes, José, Ana e Lúcia, pesando, respectivamente, 420 N, 400 N e 440 N, estão sentados sobre uma gangorra. A gangorra é de material homogêneo, e seu ponto central O está apoiado em um suporte. De um lado da gangorra estão José e Ana, distantes do ponto O, respectivamente, 1,0 m e 1,7 m, equilibrando a gangorra na horizontal com Lúcia do outro lado. Nestas condições, desprezando efeitos devidos às dimensões dos jovens, a distância de Lúcia ao ponto O é igual

  1. 3,0 m
  2. 1,0 m
  3. 2,7 m
  4. 2,5 m
  5. 1,7 m

Resposta: D

Resolução:

Para que a gangorra esteja em equilíbrio, o somatório dos momentos das forças que atuam sobre ela deve ser zero.

O momento de uma força é calculado pelo produto da força pela distância ao ponto de apoio.

No caso da gangorra, o ponto de apoio é o ponto O.

Os momentos das forças de José e Ana são iguais e opostos, portanto, eles se anulam.

O momento da força de Lúcia é dado por:

M = F * d

Onde:

F: força de Lúcia

d: distância de Lúcia ao ponto O

Para que a gangorra esteja em equilíbrio, o momento da força de Lúcia deve ser igual ao momento das forças de José e Ana. Portanto, temos:

M = F * d

(420 + 400) = 440 * d

d = 2,5 m

Portanto, a distância de Lúcia ao ponto O é igual a 2,5 m.

Explicação detalhada

Para que a gangorra esteja em equilíbrio, o somatório dos momentos das forças que atuam sobre ela deve ser zero.

O momento de uma força é calculado pelo produto da força pela distância ao ponto de apoio.

No caso da gangorra, o ponto de apoio é o ponto O.

Os momentos das forças de José e Ana são iguais e opostos, portanto, eles se anulam.

O momento da força de Lúcia é dado por:

M = F * d

Onde:

F: força de Lúcia

d: distância de Lúcia ao ponto O

Para que a gangorra esteja em equilíbrio, o momento da força de Lúcia deve ser igual ao momento das forças de José e Ana. Portanto, temos:

M = F * d

(420 + 400) = 440 * d

d = 2,5 m

Portanto, a distância de Lúcia ao ponto O é igual a 2,5 m.

Outra maneira de resolver o problema

Outra maneira de resolver o problema é considerar que a gangorra é um sistema isolado e que a resultante das forças que atuam sobre ela é zero.

As forças que atuam sobre a gangorra são:

O peso de José: 420 N

O peso de Ana: 400 N

O peso de Lúcia: 440 N

A força de reação do ponto de apoio: R

A força de reação do ponto de apoio é igual à soma das forças de José, Ana e Lúcia. Portanto, temos:

R = 420 + 400 + 440

R = 1260 N

A gangorra está em equilíbrio, portanto, a resultante das forças que atuam sobre ela é zero. Portanto, temos:

R - 420 - 400 - 440 = 0

R = 1260

(420 + 400 + 440) = 1260

d = 2,5 m

10. (FGV-SP) Em um poste, uma trave horizontal feita de madeira serve desuporte para os três isoladores de alta tensão, responsáveis, também, por manter os fios sobrelevados.

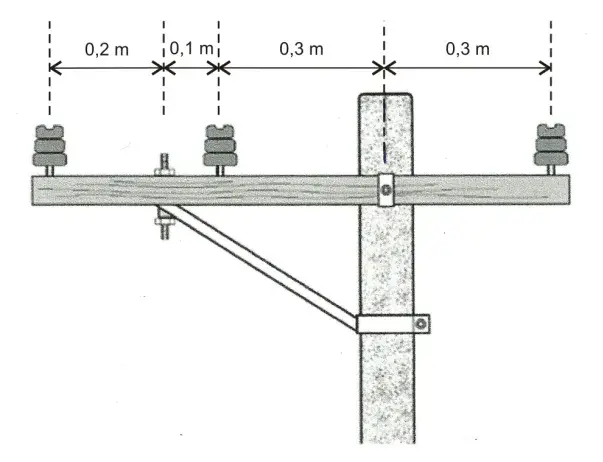
Os pesos da trave e dos isoladores podem ser considerados desprezíveis. Cada fio exerce sobre seu isolador uma força vertical de intensidade 400 N e, por essa razão, além da trave ser presa diretamente ao poste, uma haste inclinada exerce um esforço adicional para cima, em newtons, de intensidade

  1. 100
  2. 200
  3. 300
  4. 400
  5. 600

Resposta: E

Resolução:

De acordo com o enunciado, os pesos da trave e dos isoladores podem ser considerados desprezíveis. Portanto, o único peso que atua na trave é o peso da haste inclinada.

A haste inclinada exerce uma força vertical para cima na trave, que é igual ao peso da haste. O peso da haste é igual à soma dos pesos dos três isoladores, que é igual a 3 * 400 N = 1200 N.

Portanto, a força adicional que a haste exerce para cima tem intensidade de 600 N.

Aqui está a resolução completa da questão:

Solução:

De acordo com o enunciado, os pesos da trave e dos isoladores podem ser considerados desprezíveis. Portanto, o único peso que atua na trave é o peso da haste inclinada.

A haste inclinada exerce uma força vertical para cima na trave, que é igual ao peso da haste. O peso da haste é igual à soma dos pesos dos três isoladores, que é igual a 3 * 400 N = 1200 N.

Portanto, a força adicional que a haste exerce para cima tem intensidade de 600 N.

Explicação:

Fórmula para o equilíbrio em equilíbrio estático:

∑F = 0

Forças que atuam na trave:

Força vertical para cima da haste inclinada:

F = m * g

* Forças verticais para baixo dos isoladores:

F = 400 N

Soma das forças verticais:

F_total = F_haste + F_iso1 + F_iso2 + F_iso3

Substituindo as equações das forças verticais:

F_total = m * g + 400 N + 400 N + 400 N

Considerando que os pesos da trave e dos isoladores podem ser considerados desprezíveis:

F_total = 0 + 400 N + 400 N + 400 N

Resolvendo a equação:

F_total = 1200 N

Portanto, a força adicional que a haste exerce para cima tem intensidade de:

F_haste = F_total / 2 = 1200 N / 2 = 600 N

Clique Para Compartilhar Esta Página Nas Redes Sociais



Você acredita que o gabarito esteja incorreto? Avisa aí 😰| Email ou WhatsApp

Conheça nossos grupos no WhatsApp