Equilíbrio dos Corpos Extensos

01. (Unic-MT) A barra homogênea de peso P=2000N está em equilíbrio sobre dois apoios. A força de reação no ponto B vale:

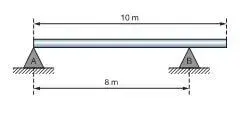
1. 2000N
2. 1000N
3. 1500N
4. 1250N
5. 2250N

02. (Med. Catanduva-SP) Uma barra AB, homogênea e de secção reta e uniforme, de 80 cm de comprimento e peso 50 N, está apoiada num ponto O, como mostra a figura. O peso Q é de 100 N. Para o equilíbrio horizontal da barra AB, deve-se suspender à extremidade A um peso de:

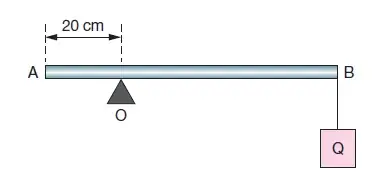
1. 150 N
2. 250 N
3. 350 N
4. 500 N
5. 400 N

03. (UEL-PR) Numa academia de ginástica, dois estudantes observam uma barra apoiada em dois pontos e que sustenta duas massas de 10 kg, uma de cada lado, conforme a figura a seguir

Após consultarem o professor, obtiveram a informação de que a massa da barra era 12 kg. Dessa forma, concluíram que seria possível acrescentar em um dos lados da barra, junto à massa já existente e sem que a barra saísse do equilíbrio, uma outra massa de, no máximo:

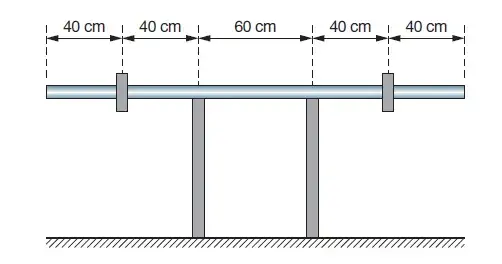
1. 10 kg
2. 12 kg
3. 20 kg
4. 24 kg
5. 30 kg

04. (UFT) A figura a seguir ilustra dois objetos de massa m e M apoiados em uma gangorra a distâncias distintas do ponto de equilíbrio. A massa M é maior que a massa m.

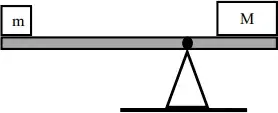
A condição de equilíbrio observada na figura ocorre, pois

1. as resultantes das forças e dos torques são nulas
2. as resultantes das forças e dos torques produzem aceleração angular.
3. a força peso do objeto de massa M produz um torque resultante no sentido horário.
4. a força peso do objeto de massa m produz um torque resultante no sentido anti-horário.

05. (Cefet-PR) Um menino que pesa 200 N, caminha sobre uma viga homogênea, de secção constante, peso de 600 N e apoiada simplesmente nas arestas de dois corpos prismáticos. Como ele caminha para a direita, é possível prever que ela rodará em torno do apoio B. A distância de B em que tal fato acontece, é, em metros, igual a:

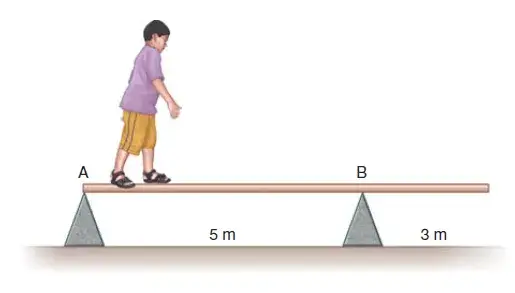
1. 0,5
2. 1
3. 1,5
4. 2
5. 3

06. (MACK-SP) Após uma aula sobre o “Princípio das Alavancas”, alguns estudantes resolveram testar seus conhecimentos num playground, determinando a massa de um deles. Para tanto, quatro sentaram-se estrategicamente na gangorra homogênea da ilustração, de secção transversal constante, com o ponto de apoio em seu centro, e atingiram o equilíbrio quando se encontravam sentados nas posições indicadas na figura. Dessa forma, se esses estudantes assimilaram corretamente o tal princípio, chegaram à conclusão de que a massa desconhecida, do estudante sentado próximo à extremidade B, é:

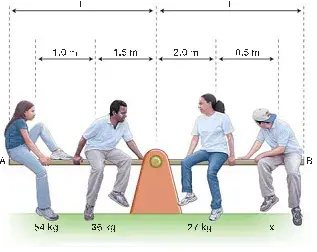
1. 108 kg
2. 63 kg
3. 54 kg
4. 36 kg

07. (EEAR) Dois garotos de massas iguais a 40 kg e 35 kg sentaram em uma gangorra de 2 metros de comprimento para brincar. Os dois se encontravam à mesma distância do centro de massa e do apoio da gangorra que coincidiam na mesma posição. Para ajudar no equilíbrio foi usado um saco de 10 kg de areia. Considerando o saco de areia como ponto material, qual a distância, em metros, do saco de areia ao ponto de apoio da gangorra?

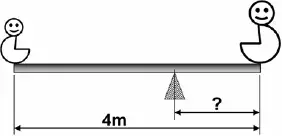
1. 2,0
2. 1,5
3. 1,0
4. 0,5

08. (ETEC) Marcelo decidiu construir uma gangorra para poder brincar com seu filho. Sobre um cavalete, ele apoiou uma tábua de modo que, quando ambos se sentassem, estando cada um em um dos extremos da tábua e sem tocar os pés no chão, a gangorra pudesse ficar equilibrada horizontalmente, sem pender para nenhum dos lados. Considerou também o fato de que seu peso era três vezes maior que o de seu filho, e que a distância entre os locais onde ele e o filho deveriam se sentar era de 3,2 m.

De acordo com essas considerações, a distância entre o ponto onde o filho de Marcelo deve se sentar e o ponto de apoio da tábua no cavalete é, aproximadamente, de

Despreze o peso da tábua, bem como as dimensões dos corpos de Marcelo e de seu filho

1. 0,8 m.
2. 1,2 m.
3. 1,6 m.
4. 2,0 m.
5. 2,4 m.

09. (UERJ) Um sistema é constituído por seis moedas idênticas fixadas sobre uma régua de massa desprezível que está apoiada na superfície horizontal de uma mesa, conforme ilustrado abaixo. Observe que, na régua, estão marcados pontos equidistantes, numerados de 0 a 6.

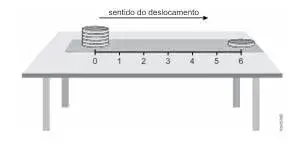
Ao se deslocar a régua da esquerda para a direita, o sistema permanecerá em equilíbrio na horizontal até que determinado ponto da régua atinja a extremidade da mesa.

De acordo com a ilustração, esse ponto está representado pelo seguinte número:

1. 4
2. 3
3. 2
4. 1

10. (ETEC) A Op Art ou “arte óptica” é um segmento do Cubismo abstrato que valoriza a ideia de mais visualização e menos expressão. É por esse motivo que alguns artistas dessa vertente do Cubismo escolheram o móbile como base de sua arte.

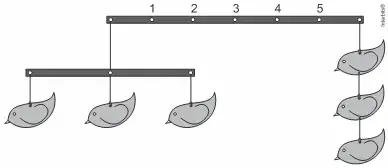
No móbile representado, considere que os “passarinhos” tenham a mesma massa e que as barras horizontais e os fios tenham massas desprezíveis.

Para que o móbile permaneça equilibrado, conforme a figura, a barra maior que sustenta todo o conjunto deve receber um fio que a pendure, atado ao ponto numerado por

1. 1
2. 2
3. 3
4. 4
5. 5