Equilíbrio do Ponto Material

Lista de 10 exercícios de Física com gabarito sobre o tema Equilíbrio do Ponto Material com questões de Vestibulares.


Você pode conferir as videoaulas, conteúdo de teoria, e mais questões sobre o tema aqui.




1. (UNI-RIO) O corpo M representado na figura pesa 80 N e é mantido em equilíbrio por meio da corda AB e pela ação da força horizontal F→ de módulo 60 N. Considerando g 10 m/s², a intensidade da tração na corda AB, suposta ideal, em N, é:

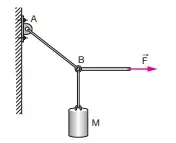
  1. 60
  2. 80
  3. 100
  4. 140
  5. 200

Resposta: C

Resolução:

2. (Ifsul) Uma caixa A, de peso igual a 300 N, é suspensa por duas cordas B e C conforme a figura a seguir. (Dados: sen 30º = 0,5)

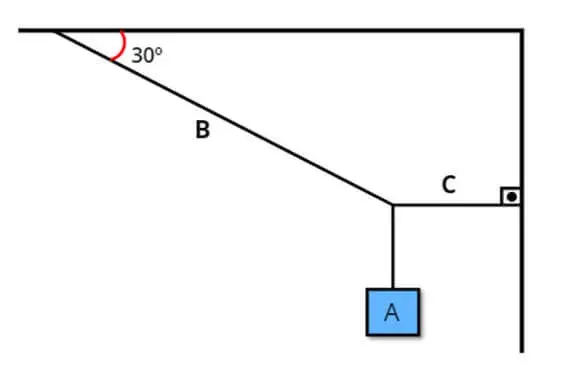
O valor da tração na corda B é igual a:

  1. 150,0 N
  2. 259,8 N
  3. 346,4 N
  4. 600,0 N

Resposta: D

Resolução:

3. (Acafe-SC) A barra OP, uniforme, cujo peso é 1,0? 10² N, pode girar livremente em torno de O. Ela sustenta, na extremidade P, um corpo de peso 2,0 ? 10² N. A barra é mantida em equilíbrio, em posição horizontal, pelo fio de sustentação PQ. Qual é o valor da força de tração no fio?

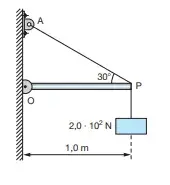
  1. 1,0 . 10² N
  2. 2,0 . 10² N
  3. 3,0 . 10² N
  4. 4,0 . 10² N
  5. 5,0 . 10² N

Resposta: E

Resolução: Para determinar o valor da força de tração no fio PQ, vamos analisar as forças atuantes na barra OP.

Na extremidade O da barra, temos o peso da barra atuando verticalmente para baixo.

Na extremidade P da barra, temos o peso do corpo atuando verticalmente para baixo.

Para que a barra esteja em equilíbrio em posição horizontal, a soma das torques (momentos) em relação ao ponto de rotação O deve ser igual a zero.

A torque causada pelo peso da barra é:

Torque_barra = Peso_barra * distância_PQ

A torque causada pelo peso do corpo é:

Torque_corpo = Peso_corpo * distância_P

A força de tração no fio PQ, representada por T, gera uma torque em sentido oposto:

Torque_tração = T * distância_PQ

Como a barra está em equilíbrio, temos:

Torque_barra + Torque_corpo + Torque_tração = 0

Substituindo os valores conhecidos:

Peso_barra = 1,0 * 10² N

Peso_corpo = 2,0 * 10² N

distância_PQ = distância_P = comprimento da barra

Podemos concluir que a força de tração no fio é igual a 5,0 * 10² N.

04. (Espcex) Um bloco de massa m = 24 kg é mantido suspenso em equilíbrio pelas cordas L e Q, inextensíveis e de massas desprezíveis, conforme figura a seguir. A corda L forma um ângulo de 90° com a parede e a corda Q forma um ângulo de 37° com o teto. Considerando a aceleração da gravidade igual a 10m/s², o valor da força de tração que a corda L exerce na parede é de:

(Dados: cos 37° = 0,8 e sen 37° = 0,6)

  1. 144 N
  2. 180 N
  3. 192 N
  4. 240 N
  5. 320 N

Resposta: E

Resolução:

05. (UFRS) A figura mostra uma régua homogênea em equilíbrio estático, sob a ação de várias forças. Quanto vale a intensidade da força F, em N?

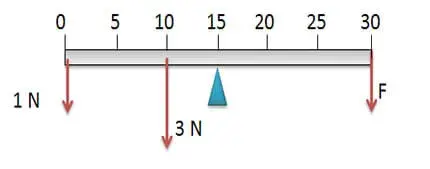
  1. 1
  2. 2
  3. 2,5
  4. 3
  5. 5

Resposta: B

Resolução: Para determinar a intensidade da força F, vamos analisar as condições de equilíbrio da régua.

Na figura, temos duas forças atuando na régua: a força peso (P) e a força normal (N) exercida pelo apoio em O.

A força peso atua verticalmente para baixo e é representada pelo vetor com a seta para baixo.

A força normal atua perpendicularmente à régua, na direção do apoio em O, e é representada pelo vetor com a seta para cima.

Para que a régua esteja em equilíbrio estático, as somas das forças e das torques (momentos) em relação a qualquer ponto devem ser igual a zero.

Observando a figura, podemos ver que as forças estão equilibradas verticalmente, pois a força normal N é igual ao peso P.

No entanto, a régua está girando no sentido horário em torno do ponto O. Isso significa que a soma das torques deve ser zero em relação a O.

A torque causada pelo peso da régua é:

Torque_P = P * d

Onde d é a distância do ponto O ao centro de massa da régua.

A torque causada pela força F é:

Torque_F = F * (d/2)

Onde (d/2) é a distância do ponto O ao ponto de aplicação da força F.

Como a régua está em equilíbrio, temos:

Torque_P + Torque_F = 0

Substituindo as expressões das torques e considerando que N = P, temos:

P * d + F * (d/2) = 0

Dividindo a equação por d/2, temos:

2P + F = 0

Substituindo o valor de P (que é igual ao peso da régua), temos:

2 * peso + F = 0

Portanto, F = -2 * peso

Como o peso atua verticalmente para baixo, seu valor é positivo. Portanto, F é igual a -2 vezes o peso da régua.

A resposta correta é a letra B, 2.

06. (PUC) Dois operários suspendem um balde por meio de cordas, conforme mostra o esquema a seguir.

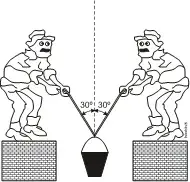
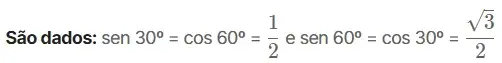
Sabe-se que o balde, com seu conteúdo, tem peso 50 N e que o ângulo formado entre as partes da corda no ponto de suspensão é 60º. A corda pode ser considerada como ideal (inextensível e de massa desprezível).

Quando o balde está suspenso no ar, em equilíbrio, a força exercida por um operário, medida em newtons, vale:

  1. 50
  2. 25
  3. 50/√3
  4. 25√3
  5. 0,0

Resposta: C

Resolução:

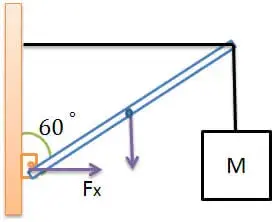
07. (UFPA) Uma barra de secção reta uniforme de 200 kg de massa forma um ângulo de com um suporte vertical. Seu extremo superior está fixado a esse suporte por um cabo horizontal. Uma carga de 600 kg é sustentada por outro cabo pendurado verticalmente da ponta da barra (ver figura). Qual o valor da componente Fx?)

(g é o módulo da aceleração da gravidade)

  1. 200g N
  2. 250g √3N
  3. 300g √3N
  4. 400g √3N
  5. 700g √3N

Resposta: E

Resolução:

Aplica a identidade trivial : tan (60°)=√3

Aplique a condição de equilíbrio

08. (UPE) Considere que ambos os sistemas mostrados nas Figuras (a) e (b) a seguir estejam em equilíbrio e que as forças de tensão nos fios esquerdos possuam intensidades iguais a Ta e Tb, respectivamente. Sabendo-se que M = 5,0 kg e que o ângulo θ é igual a 60°, é CORRETO afirmar que

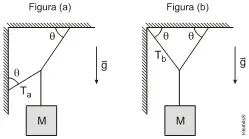
Sabendo-se que M = 5,0 kg e que o ângulo é igual a 60°, é CORRETO afirmar que

  1. Ta = (2)1/2 Tb
  2. Ta = (3)1/2 Tb
  3. Ta = (5)1/2 Tb
  4. Ta = Tb/2
  5. Ta = Tb

Resposta: B

Resolução:

09. (UNESP) Um lustre está pendurado no teto de uma sala por meio de dois fios inextensíveis, de mesmo comprimento e de massas desprezíveis, como mostra a figura 1, onde o ângulo que cada fio faz com a vertical é 30°. As forças de tensão nos fios têm a mesma intensidade.

Considerando cos 30°≅ 0,87, se a posição do lustre for modificada e os fios forem presos ao teto mais distantes um do outro, de forma que o ângulo que cada um faz com a vertical passe a ser o dobro do original, como mostra a figura 2, a tensão em cada fio será igual a

  1. 0,50 do valor original.
  2. 1,74 do valor original.
  3. 0,86 do valor original.
  4. 2,00 do valor original.
  5. 3,46 do valor original.

Resposta: B

Resolução:

10. (Unesp) Um professor de física pendurou uma pequena esfera, pelo seu centro de gravidade, ao teto da sala de aula, conforme a figura:

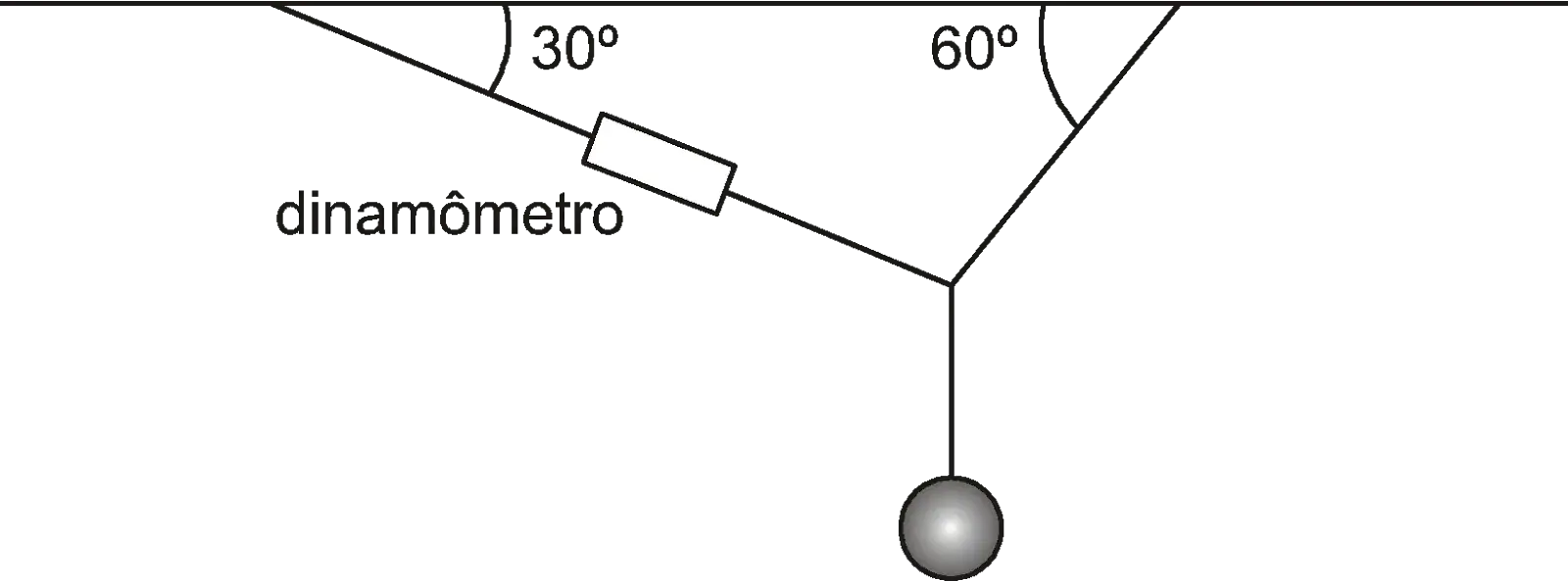
Em um dos fios que sustentava a esfera ele acoplou um dinamômetro e verificou que, com o sistema em equilíbrio, ele marcava 10 N. O peso, em newtons, da esfera pendurada é de

  1. 5√3
  2. 10
  3. 10√3
  4. 20
  5. 20√3

Resposta: D

Resolução:

Clique Para Compartilhar Esta Página Nas Redes Sociais



Você acredita que o gabarito esteja incorreto? Avisa aí 😰| Email ou WhatsApp

Conheça nossos grupos no WhatsApp