Progressões
Lista de 10 exercícios de Matemática com gabarito sobre o tema Progressões com questões da Fuvest.
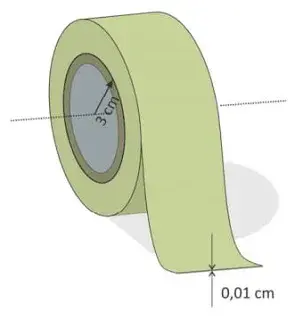
01. (Fuvest 2020) O cilindro de papelão central de uma fita crepe tem raio externo de 3 cm. A fita tem espessura de 0,01 cm e dá 100 voltas completas.
Considerando que, a cada volta, o raio externo do rolo é aumentado no valor da espessura da fita, o comprimento total da fita é de, aproximadamente,
 Note e adote:
π ≅ 3,14.
Note e adote:
π ≅ 3,14.
- 9,4 m.
- 11,0 m.
- 18,8 m.
- 22,0 m.
- 25,1 m.
02. (Fuvest 2015) Dadas as sequências
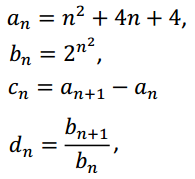
definidas para valores inteiros positivos de n, considere as seguintes afirmações:
I. an é uma progressão geométrica;
II. bn é uma progressão geométrica;
III. cn é uma progressão aritmética;
IV. dn é uma progressão geométrica.
São verdadeiras apenas
- I, II e III.
- I, II e IV.
- I e III.
- II e IV.
- III e IV.
03. (Fuvest 2010) Os números a1, a2, a3 formam uma progressão aritmética de razão r, de tal modo a1 + 3, a2 - 3, a3 - 3 estejam em progressão geométrica.
Dado ainda que a1 > 0 e a2 = 2, conclui-se que r é igual a
- 3 + √3
- 3 +
- 3 +
- 3 -
- 3 - √3
04. (FUVEST 2009) Os comprimentos dos lados de um triângulo ABC formam umaPA.
Sabendo-se também que o perímetro de ABC vale 15 e que o ângulo  mede 120°, então o produto dos comprimentos dos lados é igual a
- 25
- 45
- 75
- 105
- 125
05. (Fuvest 2008) Sabe-se sobre a progressão geométrica a1, a2, a3,... que a1 0 e a6 = −9√3.
Além disso, a progressão geométrica a1, a5, a9, ... tem razão igual a 9.
Nessas condições, o produto a2. a7 vale
- -27√3
- −3√3
- −√3
- 3√3
- 27√3
06. (FUVEST 2005) Três números positivos, cuja soma é 30, estão em progressão aritmética. Somando-se, espectivamente, 4, −4 e −9 aos primeiro, segundo e terceiro termos dessa progressão aritmética, obtemos três números em progressão geométrica. Então, um dos termos da progressão aritmética è :
- 9
- 11
- 12
- 13
- 15
07. (Fuvest) Sejam a e b números reais tais que:
(i) a, b e a + b formam, nessa ordem, uma PA;
(ii) 2ª, 16 e 2b formam PG. então o valor de a é:
08. (Fuvest 2004) Um número racional r tem representação decimal da forma r = a1 a2 a3 onde 1 ≤ a1 ≤ 9, 0 ≤ a2 ≤ 9, 0 ≤ a3 ≤ 9.
Supondo-se que:
• a parte inteira de r é o quádruplo de a3,
• a1, a2, a3 estão em progressão aritmética,
• a2 é divisível por 3,
então a3 vale:
- 1
- 3
- 4
- 6
- 9
09. (Fuvest 2001) Uma progressão aritmética e uma progressão geométrica têm, ambas, o primeiro termo igual a 4, sendo que os seus terceiros termos são estritamente positivos e iguais. o segundo termo da PA excede o segundo termo da pg em 2. qual o terceiro termo das progressões?
- 10
- 12
- 14
- 16
- 18
10. (FUVEST 2000) Sejam a, b, c três números estritamente positivos em progressão aritmética.
Se a área do triângulo ABC, cujos vértices são A = (-a, 0), B = (0, b) e C = (c, 0), é igual a b, então o valor de b é:
- 5
- 4
- 3
- 2
- 1