Pressão Hidrostática (Teorema de Stevin)
A hidrostática é a parte da física que estuda os fluidos em repouso. Apesar de a palavra "hidrostática" significar "estática da água", este termo é utilizado para designar a estática dos fluidos em geral. Wikipédia

Pressão Hidrostática
1. Pressão Manométrica
A experiência de Torricelli, vista aula anterior, confirma que a pressão aumenta a medida que a profundidade no interior de um líquido aumenta. De fato quanto mais profundo for um oceano, por exemplo, maior será a coluna de água, e maior será a pressão.
Contudo outra pergunta pode ser feita ainda: o que aconteceria se ao invés de mercúrio, Torricelli tivesse usado água? A resposta desta questão está ligada ao conceito de densidade.
O que se observa é que a diminuição da densidade é acompanhada por uma diminuição na pressão, por isso, há uma relação entre densidade e pressão.
Para encontrar esta relação, vamos analisar a coluna de fluido ilustrada na Figura 12.1, esta porção pode ser um volume de água em uma jarra

A diferença entre a pressão na base (P) e a pressão no topo (P0) dessa porção de líquido, é dada por:

Sendo g a aceleração da gravidade, d a densidade do líquido e h a altura da coluna de líquido. Este é conhecida como Lei de Stevin, em homenagem ao engenheiro holandês Simon Stevin (1548-1620) que foi um dos pioneiros no estudo da relação entre pressão e profundidade de um líquido.
A Lei de Stevin é utilizada em algumas aplicações como forma de medir pressões desconhecidas. Em alguns instrumentos, os manômetros, a diferença P – P0 é chamada de pressão manométrica (Pman). A pressão medida nos pneus de um carro, por exemplo, é a pressão manométrica, que representa a diferença entre a pressão no interior do pneu e a pressão atmosférica.
Na da coluna de líquido da Figura 12.1 a pressão absoluta (P) será:

O termo P0 representa a pressão atmosférica que atua sobre a coluna de líquido, enquanto que o termo dgh representa a pressão exercida pelo próprio fluido sobre sua base. Dois resultados são consequência desta expressão:
• Quanto mais denso for o fluido maior será a pressão exercida por ele.
• Quanto maior a coluna desse fluido, maior será a pressão exercida por ele total.
Exemplo 1: Qual será a pressão exercida pela água de uma jarra, cuja coluna tem 10cm (0,1m) de altura? Considere que a jarra está em uma casa localizada ao nível do mar.
Para resolver este problema consideraremos g = 10m/s2 e utilizaremos os valores da densidade da água e da pressão ao nível do mar (P0 = 1atm) apresentados na aula anterior, ou seja:

Utilizando a equação:

temos:
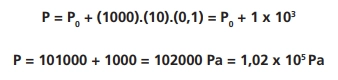
Note que a pressão absoluta foi obtida somando-se a pressão atmosférica no local, com a pressão da coluna de líquido. É importante lembrar que se a água na jarra fosse a água do mar, o valor desta pressão aumentaria, pois a densidade da água do mar é maior: d Água do mar = 1,025 x 103 kg/m3. O valor da pressão absoluta devida à água do mar neste exemplo seria: P = 102025 Pa.
Para exercitar o uso da equação para o cálculo da pressa, obtenha este valor.
2. Vasos Comunicantes
Se compararmos diferentes recipientes que contenham o mesmo líquido, as diferenças de pressão serão devidas às diferenças de altura nas colunas de líquido. Este fato pode ser ilustrado pelo comportamento dos chamados vasos comunicantes, como o ilustrado na Figura 12.2. As áreas e as formas dos recipientes não precisam ser iguais, como mostra a figura, mas suas bases são interligadas por um canal. Para uma mesma altura a pressão será a mesma.

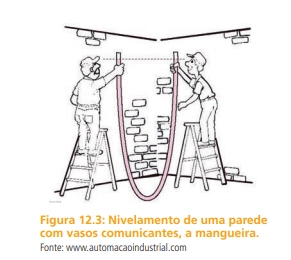
Muitas situações envolvem esse comportamento dos vasos comunicantes. O nivelamento do líquido em uma mangueira transparente é utilizado por pedreiros para nivelar uma parede, como ilustra a Figura 12.3. Os níveis de água na mangueira se equivalem quando estão à mesma altura, ou à mesma pressão, por isso se tornam uma referência para ver se dois pontos de uma mesma parede estão à mesma altura (nivelada).
As caixas d’água ficam em posições mais elevadas justamente para garantir a saída da água pela torneira. Se a caixa d’água ficasse na mesma altura da torneira não haveria diferença de pressão suficiente para que a água escoasse. A água sai da torneira por que age como se fosse equilibrar a pressão neste ponto com a pressão na caixa d’agua.
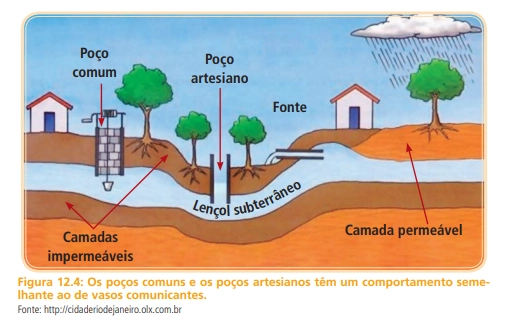
Quando se fura um poço (comum ou artesiano) é estabelecida uma configuração parecida com um vaso comunicante, Figura 12.4. O lençol de água subterrâneo (que muitas vezes é chamado de aquífero ou lençol freático) comporta-se como o canal entre os vasos. Assim como a água em um vaso comunicante, a água do poço sobe até certo nível para equilibrar a pressão.
Resumo
Nesta aula você estudou que a densidade de um fluido também interfere no comportamento da pressão. A altura da coluna de fluido pode ser utilizada para a realização de medidas de pressão. O comportamento da pressão de fluidos em vasos comunicantes oferece algumas vantagens em nosso cotidiano.
Lista Geral de Questões
Referências:
WILLIAN DA SILVA, Adriano; MARIA DOS SANTOS, Angela; BURKARTER, Ezequiel. Física I. Curitiba-PR: Instituto Federal do Paraná, 2011.
Mais Artigos
| Ângulos | Matemática Financeira |
| Expressões Numéricas | Equação do Primeiro Grau |
| Equação do 2º grau | Razão e Escala |
| Progressões Aritméticas | Proporção e Regra de três |
Biologia
| Glicídio | Lipídios |
| Proteínas | Sais Minerais |
| Membrana Plasmática | Programas de Saúde |
| Doenças: Bactérias | Doenças: Protozoários |
| Doenças: Vírus |
Física
Teoria: Química Geral
Teoria: Química Inorgânica
| Óxidos básicos | Óxidos ácidos ou anidridos |
| Óxidos neutros | Óxidos anfóteros |
| Óxidos duplos ou mistos |
Geografia
| Calor e Temperatura | Climatologia |
| Deslizamentos | El Niño e La Niña |
| Enchentes | Ilhas de Calor |
| Lixo Urbano | Ondas de calor |
| Saneamento | Sensação Térmica |
| Urbanização |
Blog HB: Colônia
História
| Egito Antigo | Fenícios |
| Hebreus | Mesopotâmia |
| Persas | Pré-História |
| Absolutismo Francês | Origem e Expansão do Islã |
| Colonização da América Inglesa | Império Bizantino |
História da Arte
| Impressionismo | Barroco Mineiro |
| Principais Movimentos Artísticos do Século XX |
Literatura
| Leituras Obrigatórias da Fuvest 2022 |
| Leituras Obrigatórias da UERJ |
| Leituras Obrigatórias da UFRGS: |
Literatura
| Trovadorismo | Classicismo |
Português
| Interpretação de Textos | Figuras de Linguagem |
| Funções de Linguagem | Variação Linguística |
Aplicativos I
Produtividade
Guia de Estudos
Mais Artigos
Aplicativos: Idiomas
Canais do Youtube Para Aprender
Tecnologia
| Baixar Livros de Graça | Fontes de Informação |
| Melhores Sites Sobre Ciências | Cursos Grátis Com Certificado |
| Telegram Para os Estudos |
Mais Artigos
| Agenda do Estudante Pro | RevisApp |
| Study | Aplicativo Pomodoro Timer |
| Trello |
Ciências
| A evolução da leishmania brasileira | Dia Mundial da doença de Chagas |
| Doenças Tropicais Negligenciadas | O papel de crianças na transmissão do novo coronavírus |