Densidade e Pressão

Densidade e Pressão
A densidade é a relação entre a massa de um objeto e o seu volume. Ela é geralmente expressa em unidades de massa por unidade de volume, como kg/m³ ou g/cm³. A densidade de um objeto pode ser calculada usando a fórmula: densidade = massa / volume.
A pressão é a força por unidade de área. Ela é geralmente medida em unidades de força por unidade de área, como N/m² ou Pascals (Pa). A pressão pode ser causada por uma força aplicada sobre um objeto, como a pressão exercida por um fluido em um recipiente. A pressão também pode ser causada por peso, como a pressão exercida pelo ar sobre uma superfície. A pressão pode ser calculada usando a fórmula: pressão = força / área.
1. Fluidos
Os conceitos que estudaremos nesta aula e nas próximas são aplicados em estudos do movimento ou equilíbrio de líquidos ou gases. Estes dois tipos de materiais pertencem a uma classe de materiais chamada de fluidos. Todo material que escoa (ou escorre), como a água numa cachoeira, pode ser considerado um fluido. Outro exemplo de fluido é a brisa que sopra do mar, pois é composta pelo ar que escoa na direção do continente.

Uma das áreas da Física que estuda as propriedades dos fluidos é a Hidrostática, onde são estudadas situações ligadas ao chamado equilíbrio estático de fluidos (condição em que está em repouso). A Hidrostática estuda, por exemplo, em que condições um barco pode flutuar sobre a água. Outra área de estudos dos fluidos em Física é a Hidrodinâmica, que estuda o movimento de fluidos. A Hidrodinâmica trata, por exemplo, do estudo do movimento de água no interior de canos em um sistema de irrigação de uma plantação.
Um dos fatores utilizados para estudar o equilíbrio ou ainda o escoamento de um fluido é a pressão. Por isso vamos estudar este conceito e algumas de suas manifestações.
2. Pressão

Você já andou de bicicleta na areia da praia? Se sua resposta é sim, deve ter percebido que os pneus afundam na areia. Qual seria a solução? Um possibilidade seria o uso de pneus mais largos. Mas por quê? Vamos pensar em outra situação e ver se encontramos a resposta. Se você tiver que cortar um pedaço de carne, vai usar uma faca afiada ou uma faca sem afiar? Qual é a diferença da faca afiada para aquela não foi afiada? Mas qual é a relação entre o fio da faca e largura dos pneus da bicicleta?
Note, em ambos os casos há uma diferença entres as áreas de contato. No caso da bicicleta, quanto mais largo for o pneu, menos ele afunda na areia. No caso da carne, o fio da faca afiada é bem mais fino que fio da faca sem afiar.
O ponto comum entre os dois eventos é então a área de contato (A), pois as forças envolvidas nestes eventos não mudam: o peso do ciclista é sempre o mesmo e a força que você usaria pra cortar a carne também. O fato é que quanto menor a área de contato mais fácil afundar ou cortar.
Esta influência da área de contato está ligada a uma grandeza chamada Pressão, que é definida como a razão entre a força aplicada e a área onde esta força é aplicada. Esta definição é matematicamente escrita na equação a seguir:
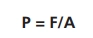
Como você viu anteriormente, a unidade de medida de força é o Newton (N) e a unidade de medida de área é o metro quadrado (m²), por isso, a unidade de medida de pressão deve ser Newton por metro quadrado (N/m²). Para facilitar a leitura das medidas de pressão esta unidade recebeu um nome, o pascal. Por isso, no Sistema Internacional (SI) a unidade de pressão é o pascal (Pa), sendo:
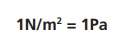
Exemplo 1:
Considere um bloco de concreto de massa 100Kg, cujas faces possuem áreas de 2m² e 4m². Qual das faces exerce maior pressão sobre o chão?
Como a massa do bloco é de 1000Kg podemos calcular o seu peso usando g = 10m/s² e fazendo:
Peso = 100 x 10 = 1000N.
Vamos chamar a face de 2m² de face 1 e calcularemos a pressão P1 exercida por esta face:
P1 = 1000 N/2m² = 500Pa.
Adotando o mesmo procedimento calculamos a pressão P2 da outra face:
P2 = 1000 N/4m² = 250 Pa.
Pelos nossos cálculos percebemos que a face de maior área (4m²) exerce menor pressão.
3. Tensão Superficial
Os líquidos em geral possuem em sua superfície uma concentração de moléculas que acabam formam algo como uma película, como se os líquidos fossem envolvidos por uma embalagem plástica. Esta espécie de película constitui na verdade uma rede de forças que atuam na superfície dos líquidos, chamada tensão superficial.

Observe na Figura que o inseto que caminha sobre a água
Insetos
Normalmente o inseto afundaria, mas devido à tensão superficial, o peso do inseto apenas deforma a superfície da água e pode caminha sobre ela. Tal é a importância da tensão superficial que muitos dos insetos que caminham sobre a água, acabam se tornando alimento para os peixes.
Mergulhar na água
Quando alguém mergulha na água recomenda-se que não pule de barriga (ou de peito), pois o efeito pode ser bem dolorido. Para mergulhar você deve romper a tensão superficial (lembre-se ela é como uma camada de plástico sobre a água), e isso se faz aumentando a pressão exercida por seu corpo.
O ato de pular na água com os braços esticados e juntos na direção da água faz com que seu peso esteja concentrado na ponta dos dedos. Como a área da ponta dos dedos é pequena a pressão exercida é grande e o mergulho não é dolorido. É como se suas mãos abrissem a água para você entrar.

Quando alguém mergulha na água recomenda-se que não pule de barriga (ou de peito), pois o efeito pode ser bem dolorido
Formato dos barcos
O formato dos barcos, também favorece o rompimento da tensão superficial, pois a parte da frente é mais fina, o que facilita a locomoção.

Densidade
Você já deve ter observado que materiais diferentes, mesmo tendo os mesmos tamanhos, possuem massas diferentes. Por exemplo, uma caixa de isopor comparada com uma caixa de vidro (Figura 10.1). Embora tenham os mesmos tamanhos, a de vidro tem massa maior. Há, portanto, uma relação entre a massa o objeto e o material do qual ele é feito. Qual será essa relação?

Podemos ainda pensar em outra situação, para discutir este assunto: por que a rolha utilizada em uma vara de pescaria não pode ser feita de Chumbo? Você deve dizer: “ah, simples, é por que o chumbo afundaria”. Mas, por que o Chumbo afundaria? Pela mesma razão que a caixa de vidro é mais massiva que a de plástico, a densidade dos materiais.
A densidade (d) de um material é definida como a razão entre sua massa (m) e seu volume (V), como é mostrado na equação a seguir:
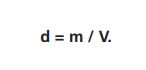
A unidade no Sistema Internacional para a densidade é o quilogramas por metro cúbico (kg/m³). Voltemos ao caso das caixas! Embora ambas tenham o mesmo volume, o vidro tem uma densidade maior do que o isopor, por isso sua massa será maior.
A densidade é uma propriedade associada a cada material, é como se fosse sua identificação. A Tabela 10.1 mostrada a seguir apresenta a densidade de alguns materiais.

Exemplo 1: Se o volume de uma placa utilizada para fazer uma caixa for de 10-³ m³, qual será a massa desta placa se: a) for feita de vidro? b) for feita de isopor? c) for feita de madeira?
Para resolver este exemplo precisamos isolar a massa (m) na equação que define a densidade, o que nos dará:

4. Pressão Atmosférica
O ambiente onde vivemos aqui na Terra é totalmente envolvido por uma massa de ar composta por oxigênio, nitrogênio, vapor d’água, além de outros compostos. Esta combinação de gases permite a nossa existência. Este ambiente, ilustrado na figura abaixo, é chamado de atmosfera. Acima da atmosfera existem outras camadas com outras composições, mas estas outras camadas não serão discutidas nesta aula.
Como o ar tem massa podemos supor que seu peso (que é uma força) exerce pressão sobre tudo que habita a atmosfera, trata-se da pressão atmosférica. Mas será que esta pressão é a mesma em todos os lugares?

5. Primeira Medida da Pressão Atmosférica
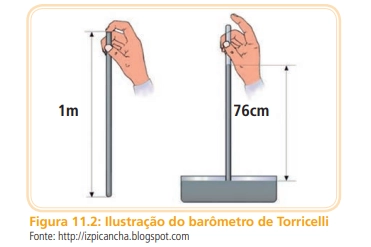
Por volta de 1646, o físico italiano Evangelista Torricelli (1608-1647) realizou um experimento com o objetivo de medir a pressão atmosférica. Torricelli encheu de mercúrio (Hg) um fino tubo de vidro com um metro de comprimento, como ilustra a Figura 11.2, e realizou o experimento que consistiu na primeira medida da pressão atmosférica.
Torricelli inverteu o tubo e o mergulhou em um recipiente que também continha mercúrio (Hg). Após este processo verificou-se que a coluna de mercúrio (Hg) descia até permanecer com a altura de 76 cm, como ilustra a mesma Figura 11.2. O sistema construído por Torricelli é, muitas vezes, chamado de Barômetro de Torricelli, e os instrumentos de medida de pressão atmosférica são, devido a este fato, chamados de Barômetros.
De acordo com a Primeira Lei de Newton, quando o sistema entra em equilíbrio a pressão atmosférica (Patm) sobre o mercúrio do recipiente é igual à pressão exercida pelo peso da coluna de mercúrio do tubo.
6. Aplicações dos Resultados de Torricelli
A experiência, realizada por Torricelli, levou a dois resultados muito importantes. O primeiro resultado foi a existência do vácuo no topo da coluna de mercúrio (no interior do tubo). Na época de Torricelli a existência do vácuo era negada por muitos estudiosos.
A ideia de vácuo está associada a um ambiente ou recipiente no qual não há matéria. Contudo, para efeitos práticos o vácuo é definido como um ambiente onde a pressão é menor do que a pressão atmosférica. Hoje o vácuo é produzido por equipamentos chamados de Bombas de Vácuo (Figura 11.3b), que extraem ar do interior de um recipiente.
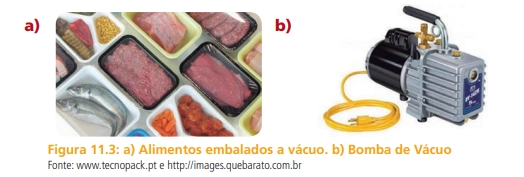
Muitas de alimentos como carnes frescas, são embalados em recipientes de vácuo. Este procedimento é adotado, para facilitar a compactação durante o armazenamento e para evitar contaminação devido a bactérias presentes no ar. A tecnologia das embalagens a vácuo melhora o padrão de conservação de alimentos por meio da diminuição do contato com oxigênio, que favorece o desenvolvimento de micróbios. As peças de carne a vácuo podem então ficar mais tempo nas gôndolas dos supermercados (Figura 11.3a).
Existem objetos que são construídos para que a pressão em seu interior seja maior que a pressão atmosférica. É o caso dos botijões de gás de cozinha, Figura 11.4. Como a pressão no interior destes recipientes é maior que a pressão atmosférica, quando ligado a um fogão o gás escoa até o local onde a chama é produzida. O escoamento é controlado por uma válvula, e qualquer abertura descontrolada pode causar vazamentos, o que é percebido pelo cheiro característico.

Outro resultado da experiência de Torricelli foi a possibilidade de medida da pressão por meio da altura da coluna de um fluido. Como a coluna de mercúrio foi de 76cm, definiu-se por meio dela o valor da pressão atmosférica ao nível do mar. Muitas vezes a pressão atmosférica é medida em centímetros de mercúrio ou em atmosferas (atm). A pressão atmosférica vale 1atm ao nível do mar, o que equivale à pressão de uma coluna de 76cm de mercúrio. Podemos relacionar estas duas unidades ao pascal, que é a unidade do SI, por meio das seguintes igualdades:
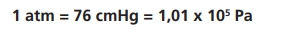
Exemplo 1: Se a pressão no interior de um botijão de gás de cozinha é de 248 cmHg qual será o valor desta pressão em pascal e em atmosfera
A conversão de unidades neste caso pode ser feito por meio de uma regra de três. Primeiro faremos a conversão para o valor em atmosferas.

Multiplicando em diagonal temos:

Adotando o mesmo procedimento na conversão para o pascal fazemos:

Por meio destas conversões percebemos que a pressão no interior de um botijão de gás é cerca de 3 vezes maior que a pressão atmosférica ao nível do mar. Este resultado mostra a necessidade de bastante cuidado na prevenção de vazamentos de gás, pois devido à esta diferença de pressão qualquer abertura na mangueira, falha na válvula ou mesmo uma boca do fogão defeituosa pode levar a um vazamento, que pode causar um acidente.
Em algumas atividades como oficinas de pintura automotiva e borracharias são utilizados equipamentos que aumentam a pressão do ar, para produzir posteriormente um jato de ar comprimido. Estes equipamentos são os compressores de ar, que, ao contrário da bomba de vácuo, sugam o ar da atmosfera e o comprimem em um recipiente. O ar comprimido proveniente de compressores pode ser utilizado em pistolas de pintura ou em bombas para encher uma boia.

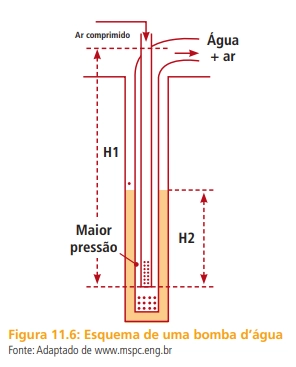
Algumas bombas d’água também se utilizam do aumento da pressão, como ilustra a Figura 11.6. Neste caso, o motor da bomba aumenta a pressão no fundo de um poço artesiano, fazendo com que a água suba pela tubulação a uma região de maior altitude.
6. Voltando à Pressão Atmosférica
Outro físico, o francês Blaise Pascal (1623-1662), realizou em 1648 experiências que mostraram que o peso do ar atmosférico é maior na base de uma montanha do que no topo desta. Na verdade, Pascal repetiu a experiência de Torricelli no alto de uma montanha e verificou que a pressão é menor a medida que a altitude aumenta. Os resultados de Pascal estão em acordo com a ideia de que a espessura da atmosfera é menor em altitudes maiores, como ilustra a figura.

Estudos realizados tomando como base os conceitos de pressão e de densidade mostraram que o ar atmosférico vai ficando cada vez menos denso a medida a altitude aumenta, ou seja, em maiores altitudes há menos ar para respirar. Costuma-se dizer que em maiores altitudes o ar é mais rarefeito, o que significa que a pressão atmosférica e a menor densidade do ar são menores.
Lista Geral de Questões
Referências:
WILLIAN DA SILVA, Adriano; MARIA DOS SANTOS, Angela; BURKARTER, Ezequiel. Física I. Curitiba-PR: Instituto Federal do Paraná, 2011.
Mais Artigos
| Ângulos | Matemática Financeira |
| Expressões Numéricas | Equação do Primeiro Grau |
| Equação do 2º grau | Razão e Escala |
| Progressões Aritméticas | Proporção e Regra de três |
Biologia
| Glicídio | Lipídios |
| Proteínas | Sais Minerais |
| Membrana Plasmática | Programas de Saúde |
| Doenças: Bactérias | Doenças: Protozoários |
| Doenças: Vírus |
Física
Teoria: Química Geral
Teoria: Química Inorgânica
| Óxidos básicos | Óxidos ácidos ou anidridos |
| Óxidos neutros | Óxidos anfóteros |
| Óxidos duplos ou mistos |
Geografia
| Calor e Temperatura | Climatologia |
| Deslizamentos | El Niño e La Niña |
| Enchentes | Ilhas de Calor |
| Lixo Urbano | Ondas de calor |
| Saneamento | Sensação Térmica |
| Urbanização |
Blog HB: Colônia
História
| Egito Antigo | Fenícios |
| Hebreus | Mesopotâmia |
| Persas | Pré-História |
| Absolutismo Francês | Origem e Expansão do Islã |
| Colonização da América Inglesa | Império Bizantino |
História da Arte
| Impressionismo | Barroco Mineiro |
| Principais Movimentos Artísticos do Século XX |
Literatura
| Leituras Obrigatórias da Fuvest 2022 |
| Leituras Obrigatórias da UERJ |
| Leituras Obrigatórias da UFRGS: |
Literatura
| Trovadorismo | Classicismo |
Português
| Interpretação de Textos | Figuras de Linguagem |
| Funções de Linguagem | Variação Linguística |
Aplicativos I
Produtividade
Guia de Estudos
Mais Artigos
Aplicativos: Idiomas
Canais do Youtube Para Aprender
Tecnologia
| Baixar Livros de Graça | Fontes de Informação |
| Melhores Sites Sobre Ciências | Cursos Grátis Com Certificado |
| Telegram Para os Estudos |
Mais Artigos
| Agenda do Estudante Pro | RevisApp |
| Study | Aplicativo Pomodoro Timer |
| Trello |
Ciências
| A evolução da leishmania brasileira | Dia Mundial da doença de Chagas |
| Doenças Tropicais Negligenciadas | O papel de crianças na transmissão do novo coronavírus |