Razão e Proporção
Lista de 20 exercícios de Matemática com gabarito sobre o tema Razão e Proporção com questões da Vestibulares Militares
Você pode conferir as videoaulas, conteúdo de teoria, e mais questões sobre o tema Razão e Proporção.
01. (EEAR) Após observar o clarão de um raio, uma criança cronometrou o tempo para ouvir o estrondo causado, o trovão. Contou, então, dez segundos desde avistar o clarão até ouvir o trovão. Procurando na internet, descobriu que a velocidade média do som no ar é 346 m/s.
A distância estimada da criança ao raio é melhor expressa, em metros, por:
Observação: considere a detecção do clarão pela criança como instantânea, como se a velocidade da luz fosse infinita.
- 34,6
- 123
- 3460
- 6920
02. (AFA) A figura abaixo mostra uma pequena esfera vazada E, com carga elétrica q = +2,0 ⋅10−5 C e massa 80 g, perpassada por um eixo retilíneo situado num plano horizontal e distante D = 3 m de uma carga puntiforme fixa Q = −3,0 ⋅10−6 C.
Se a esfera for abandonada, em repouso, no ponto A, a uma distância x, muito próxima da posição de equilíbrio O, tal que, << 1 a esfera passará a oscilar de MHS, em torno de O, cuja pulsação é, em rad/s, igual a
03. (EPCAR) Uma pessoa vai tomar um medicamento 3 vezes ao dia, durante 14 dias, em doses de 6 mL cada vez. Se cada frasco contém 200 cm3 do medicamento, a quantidade do segundo frasco que NÃO será utilizada é
- menor que 75%
- exatamente 75%
- maior que 76%
- exatamente 76%
04. (EEAR) Uma empresa com 280 funcionários, realizou estudos estatísticos e constatou que o seu consumo médio diário de água é de dois litros por pessoa. Determine o consumo mensal médio de água da empresa, em metros cúbicos. Considere o mês com 30 dias.
- 16,8
- 168
- 1.680
- 16.800
05. (EPCAR) Elisa pretende comprar um computador que custa x reais. Ela possui 70% do valor total do computador e ainda vai ganhar de seus avós uma herança, que será totalmente repartida entre ela e suas irmãs Daniella e Lavínia.
Nessa partilha, Elisa recebeu 0,2777... da herança, Daniella 1200 reais e Lavínia 7/18 da herança.
Ao fazer as contas do quanto possuía para comprar o computador, percebeu que ainda lhe faltavam 200 reais para realizar a compra.
O valor x do computador é, em reais, tal que o número de divisores naturais de x é
- 18
- 20
- 22
- 24
06. (AFA) Um tanque com capacidade de 300 litros de água possui duas torneira: I e II
A torneira I despeja água no tanque a uma vazão de 2l por minuto. Já a torneira II retira água do tanque a uma vazão de l por minuto.
Às 8h de certo dia, com o tanque vazio, a torneira I foi aberta e, após 15 minutos, foi fechada. Às 9h e 30min as duas torneiras foram abertas, e assim permaneceram até 11h e 30min. Neste horário a torneira II é fechada, mas a torneira I permanece aberta até o momento em que a água atinge a capacidade do tanque.
Este momento ocorre às
- 12h e 10min
- 12h e 15min
- 12h e 20min
- 12h e 25min
07. (EPCAR) As turmas FOX e GOLF do CPCAR 2018 , que possuem 30 e 20 alunos, respectivamente, combinaram viajar para uma casa de praia num feriado que aconteceu no mês de junho de 2018 .
Antes de viajar, decidiram dividir todas as despesas entre as turmas de forma diretamente proporcional ao número de alunos de cada turma.
Pagaram todas as despesas, mas não pagaram de forma proporcional. A turma FOX pagou 12000 reais e a turma GOLF pagou 10500 reais.
Tendo como base o que as turmas haviam combinado em relação às despesas da viagem, é correto afirmar que
- a despesa correta da turma GOLF seria mais de 10000 reais.
- a turma FOX pagou a menos 10% do que deveria ter pago.
- o que a turma GOLF pagou a mais é um valor maior que 1800 reais.
- a turma FOX deveria ter pago mais de 10000 reais.
08. (EPCAR) Hoje, dia 29 de julho de 2012, José tem o dobro da idade que Luiz tinha quando José tinha a idade que Luiz tem. Quando Luiz tiver a idade que José tem, a soma das idades deles será 90 anos.
Em 29 de julho de 2017, a razão entre as idades de José e Luiz, nessa ordem, será
09. (EsPCEx) Uma fábrica de tratores agrícolas, que começou a produzir em 2010, estabeleceu como meta produzir 20.000 tratores até o final do ano de 2025. O gráfico abaixo mostra as quantidades de tratores produzidos no período 2010-2017.
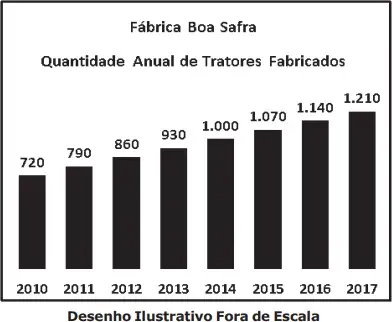
Admitindo que a quantidade de tratores produzidos evolua nos anos seguintes segundo a mesma razão de crescimento do período 2010-2017, é possível concluir que a meta prevista
- deverá ser atingida, sendo superada em 80 tratores.
- deverá ser atingida, sendo superada em 150 tratores.
- não deverá ser atingida, pois serão produzidos 1.850 tratores a menos.
- não deverá ser atingida, pois serão produzidos 150 tratores a menos.
- não deverá ser atingida, pois serão produzidos 80 tratores a menos.
10. (EPCAR) Para encher um reservatório com água, pode-se usar duas torneiras. A primeira torneira enche esse reservatório em 36 minutos. A segunda enche o mesmo reservatório em 24 minutos. Certo dia, em que esse reservatório estava vazio, a primeira torneira é aberta durante um período de k minutos. Ao fim de k minutos, a primeira torneira é fechada e abre-se, imediatamente, a segunda, que fica aberta por um período de (k + 3) minutos.
Se o volume de água atingido corresponde a da capacidade do reservatório, então o tempo total gasto foi
- 31% de hora
- 30% de hora
- 28% de hora
- 27% de hora
11. (AFA) Durante 16 horas, desde a abertura de uma certa confeitaria, observou-se que a quantidade q(t) de unidades vendidas do doce “amor em pedaço”, entre os instantes (t −1) e t, é dada pela lei q(t) = t − 8 + t −14 , em que t representa o tempo, em horas, e t ∈ {1,2,3,...,16}
É correto afirmar que
- entre todos os instantes foi vendida, pelo menos, uma unidade de “amor em pedaço”.
- a menor quantidade vendida em qualquer instante corresponde a 6 unidades.
- em nenhum momento vendem-se exatamente 2 unidades.
- o máximo de unidades vendidas entre todos os instantes foi 10
12. (EPCAR) Uma mãe dividiu a quantia de R$ 2 100,00 entre seus três filhos de 3, 5 e 6 anos. A divisão foi feita em partes inversamente proporcionais às idades de cada um.
Dessa forma, é verdade que
- o filho mais novo recebeu 100 reais a mais que a soma dos valores recebidos pelos outros dois filhos.
- o filho mais velho recebeu 20% a menos que o filho do meio.
- a quantia que o filho do meio recebeu é 40% do que recebeu o mais novo.
- se a divisão fosse feita em partes iguais, o filho mais velho teria sua parte acrescida de 40% em relação ao que realmente recebeu.
13. (EPCAR) Certa máquina, funcionando normalmente 5 horas por dia, gasta 3 dias para produzir 1200 embalagens.
Atualmente está com esse tempo de funcionamento diário reduzido em 20%, trabalhando, assim, apenas T horas por dia.
Para atender uma encomenda de 1840 embalagens, aproveitando ao máximo em todos os dias o seu tempo T de funcionamento, ela gastará no último dia
- 120 minutos
- 150 minutos
- 180 minutos
- 200 minutos
14. (AFA) Para angariar fundos de formatura, os cadetes do 1o ano da AFA vendem camisas de malha com o emblema da turma. Se o preço de venda de cada camisa é de 20 reais, eles vendem por mês 30 camisas.
Fizeram uma pesquisa e verificaram que, para cada 2 reais de desconto no preço de cada camisa, são vendidas 6 camisas a mais por mês.
Dessa forma, é correto afirmar que
- é possível fazer mais de 10 descontos de 2 reais.
- tanto faz vender as camisas por 12 reais cada uma ou 18 reais cada uma que o faturamento é o mesmo.
- o máximo faturamento ocorre se são vendidas menos de 40 camisas por mês.
- se o preço de venda de cada camisa é de 14 reais, então o faturamento é maior que 680 reais.
15. (EEAR) Dois pedreiros levaram latas cheias de concreto de mesma massa para uma laje a partir do solo. O pedreiro 1 o fez içando a lata presa por uma corda e o pedreiro 2 o fez através de uma escada, como mostra a figura:
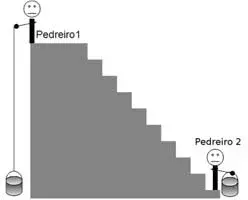
Se o pedreiro 1 subiu a lata em menor tempo que o pedreiro 2, podemos afirmar que:
- o pedreiro 2 fez um trabalho maior do que o pedreiro 1.
- o pedreiro 1 fez um trabalho maior do que o pedreiro 2.
- a potência desenvolvida pelo pedreiro 1 é maior do que a potência desenvolvida pelo pedreiro 2.
- a potência desenvolvida pelo pedreiro 2 é maior do que a potência desenvolvida pelo pedreiro 1.
16. (EPCAR) A quantidade de suco existente na cantina de uma escola é suficiente para atender o consumo de 30 crianças durante 30 dias. Sabe-se que cada criança consome, por dia, a mesma quantidade de suco que qualquer outra criança desta escola. Passados 18 dias, 6 crianças tiveram que se ausentar desta escola por motivo de saúde. É correto afirmar que, se não houver mais ausências nem retornos, a quantidade de suco restante atenderá o grupo remanescente por um período de tempo que somado aos 18 dias já passados, ultrapassa os 30 dias inicialmente previstos em
- 10%
- 20%
- 5%
- 15%
17. (AFA) Três carros, a, b e c, com diferentes taxas de consumo de combustível, percorrerão, cada um, 600 km por um mesmo caminho. No ponto de partida, os três estão com tanque cheio.
Após terem percorrido, cada um, 1/5 do total previsto, os carros b e c foram abastecidos completando novamente seus tanques e gastaram, juntos, R$ 66,00.
Ao final dos 600 km, os três carros foram abastecidos, completando seus tanques, e, nesse abastecimento, juntos, gastaram R$ 384,00.
Considerando o preço do litro do combustível usado pelos três carros a R$ 3,00, a distância que o carro a percorre, em média, com um litro de combustível é
- 12 km
- 15 km
- 16 km
- 18 km
18. (EPCAR) Certo dia, Isabela e Ana Beatriz saíram para vender pastéis na praia. Elas tinham juntas 460 pastéis. No final do dia, verificou-se que Isabela conseguiu vender 3/5 dos pastéis que levara e Ana Beatriz 5/8 dos pastéis que levara.
Ao final do dia, o número de pastéis que restou para Ana Beatriz era a metade do número de pastéis que restou para Isabela.
Se Ana Beatriz, levou x pastéis para vender, então, a soma dos algarismos de x é
- 6
- 7
- 8
- 9
19. (EPCAR) Uma fábrica de aviões levantou dados sobre sua produção e verificou que foram vendidos, no ano de 2007, 140 aviões.
A fábrica produziu três modelos de aviões: A, B e C Sabe-se que o número de aviões vendidos do modelo A é o sêxtuplo de 0,3 do quádruplo da metade do número de aviões vendidos do modelo C e os modelos B e C juntos, correspondem a 40% dos aviões vendidos.
Com base nessas informações, é INCORRETO afirmar que
- a quantidade de aviões vendidos do modelo A é 25% da quantidade de aviões vendidos do modelo C
- a quantidade de aviões dos modelos A e B vendidos é um número cuja soma dos algarismos é um número primo.
- o modelo C foi o menos vendido.
- a quantidade de aviões vendidos do modelo B é igual à quantidade de aviões vendidos do modelo C mais 1/10 do total de aviões vendidos dos modelos A, B e C juntos.
20. (EPCAR) Três operários A, B e C trabalhando juntos 8 horas por dia construíram um muro em 6 dias. Se B tivesse trabalhado sozinho, 8 horas por dia, gastaria 2/3 a mais da quantidade de dias utilizada pelos três juntos. Se A tivesse trabalhado sozinho, 4 horas por dia, gastaria o quádruplo do número de dias de B
Considerando A, B e C, cada um trabalhando 8 horas por dia, sendo mantidas as demais condições de trabalho, é correto afirmar que para construir tal muro
- um deles, isoladamente, gastaria exatamente 1 mês.
- A e B juntos gastariam mais de 7 dias.
- C gastaria sozinho menos de 1 mês e meio de trabalho.
- B e C trabalhando juntos gastariam menos de 10 dias.