Geografia Plana II
Lista de 20 exercícios de Matemática com gabarito sobre o tema Geografia Plana II com questões da Vestibulares Militares
Você pode conferir as videoaulas, conteúdo de teoria, e mais questões sobre o tema Geografia Plana II.
01. (EEAR) No quadrilátero ABCD, o valor de y – x é igual a
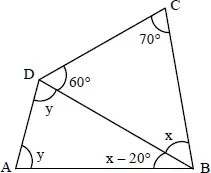
- 2x
- 2y
02. (EsPCEx) As medidas das arestas de um paralelepípedo retângulo são diretamente proporcionais a 3, 4 e 5 e a soma dessas medidas é igual a 48 cm.
Então a medida da sua área total, em cm², é
- 752
- 820
- 1024
- 1302
- 1504
03. (EEAR) Ao somar o número de diagonais e o número de lados de um dodecágono obtém-se
- 66
- 56
- 44
- 42
04. (ESA) A área do triângulo equilátero cuja altura mede 6cm é:
- 12√3 cm²
- 4√3 cm²
- 24√3 cm²
- 144cm²
- 6√3 cm²
05. (EEAR) Sabe-se que a hipotenusa de um triângulo retângulo tem 5√5 cm de comprimento e a soma dos catetos é igual a 15cm. As medidas, em cm, dos catetos são
- 6 e 9
- 2 e 13
- 3 e 12
- 5 e 10
06. (ESA) Num triângulo retângulo cujos catetos medem √8 e √9, a hipotenusa mede
- √10
- √11
- √13
- √17
- √19
07. (EEAR) O lado, o perímetro e a área de um triângulo equilátero, nesta ordem, são termos de uma Progressão Geométrica. Assim, a medida da altura desse triângulo equilátero é _______ unidades de comprimento.
- 12√3
- 6√3
- 3
- 18
08. (ESA) Um hexágono regular está inscrito em uma circunferência de diâmetro 4cm.
O perímetro desse hexágono, em cm, é
- 4π.
- 8π.
- 24.
- 6.
- 12.
09. (EEAR) Um triângulo ABC de base BC = (x + 2) tem seus lados AB e AC medindo, respectivamente, (3x - 4) e (x + 8). Sendo este triângulo isósceles, a medida da base BC é
- 4
- 6
- 8
- 10
10. (EFOMM) Seja ABC um triângulo inscrito em uma circunferência de centro O. Sejam O' e E o incentro do triângulo ABC e o ponto médio do arco BC que não contém o ponto A, respectivamente.
Assinale a opção que apresenta a relação entre os segmentos EB, EO' e EC.
- E B = EO' = EC
- EB < EO'=EC
- EB> EO' > EC
- EB = EO' > EC
- EB < EO' < EC
11. (EPCAR) A figura abaixo representa o logotipo que será estampado em 450 camisetas de uma Olimpíada de Matemática realizada entre os alunos do “Colégio Alfa”.
Essa figura é formada por um círculo de centro O inscrito num triângulo isósceles cuja base BC mede 24 cm e altura relativa a esse lado mede 16 cm
O círculo será pintado com tinta cinza e sabe-se que é necessário, exatamente, 1 pote de tinta cinza para pintar 5400 cm2
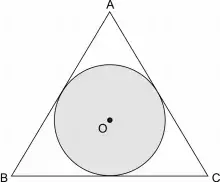
Adote π =3
Com base nesses dados, é correto afirmar que o número de potes necessários para pintar o círculo em todas as camisetas é igual a
- 9
- 10
- 11
- 12
12. (EAM) Sejam os conjuntos A = {x ∈ R; 1 ≤ x ≤ 4}, B = {y ∈ ℝ; 3 ≤ y ≤ 7}.
Considerando o conjunto A X B, (A cartesiano B) pode-se afirmar que a diagonai do polígono formado por esse conjunto é representada numericamente por:
- 2
- 3
- 4
- 5
- 6
13. (EsPCEx) Um trapézio ABCD, retângulo em A e D, possui suas diagonais perpendiculares.
Sabendo-se que os lados AB e CD medem, respectivamente, 2 cm e 18 cm, então a área, em cm², desse trapézio mede
- 120.
- 60.
- 180.
- 30.
- 240.
14. (ESA) Uma pequena praça tem o formato triangular, as medidas dos lados desse triângulo são √37m, 4m e 3m.
Qual é a medida do ângulo oposto ao maior lado?
- 120°
- 60°
- 90°
- 45°
- 150°
15. (EsPCEx) Um poliedro convexo, com 13 vértices, tem uma face hexagonal e 18 faces formadas por polígonos do tipo P.
Com base nessas informações, pode-se concluir que o polígono P é um
- dodecágono.
- octógono.
- pentágono.
- quadrilátero.
- triângulo.
16. (Colégio Naval) Seja ABCD um quadrado de lado 1 e centro em '0. Considere a circunferência e centro em '0 e raio 3/7.
A área 'S' da regiãol externa ao círculo considerado e interna ao quadrado é tal que:
- 0 ≤ S < 0,4
- 0,4 ≤ S < 0,8
- 0,8 ≤ S < 0,9
- 0,9 ≤ S < 1
- 1 ≤ S < 1,2
17. (EEAR) Sejam A(–3, 3), B(3, 1), C(5, –3) e D(–1,–2) vértices de um quadrilátero convexo. A medida de uma de suas diagonais é
- 15
- 13
- 12
- 10
18. (CN) Um ponto P, pertencente a uma circunferência de raio de 5 unidades, dista 4,8 unidades de um diâmetro dessa circunferência.
Qual a soma das distâncias de P até os extremos desse diâmetro?
- 14
- 12
- 7
- 6
- 5
19. (EsPCEx) Os centros de dois círculos distam 25 cm. Se os raios desses círculos medem 20 cm e 15 cm, a medida da corda comum a esses dois círculos é
- 12 cm.
- 24 cm.
- 30 cm.
- 32 cm.
- 36 cm.
20. (CN) Observe a figura a seguir.
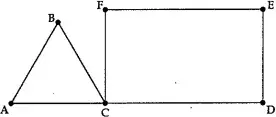
Ela apresenta o triângulo equilátero ABC e o retângulo CDEF. Sabe-se que A, C e D estão na mesma reta, AC = CF e CD = 2DE. Com centro em C e raio CD traça-se o arco de circunferência que intersecta EF em G. Por F traça-se a reta FH / / CG, de modo tal que D, G e H estejam sobre a mesma reta.
Dado que a área do triângulo CDG é 36, o valor da soma das medidas das áreas dos triângulos CBF e FGH é:
- 22
- 27
- 31
- 36
- 40