Estudo dos Gases

Lista de 10 exercícios de Química com gabarito sobre o tema Estudo dos Gases com questões do ITA/IME.




01. (ITA) Assumindo um comportamento ideal dos gases, assinale a opção com a afirmação CORRETA:

  1. De acordo com a Lei de Charles, o volume de um gás torna-se maior quanto menor for a sua temperatura.
  2. Numa mistura de gases contendo somente moléculas de oxigênio e nitrogênio, a velocidade média das moléculas de oxigênio é menor do que as de nitrogênio.
  3. Mantendo-se a pressão constante, ao aquecer um mol de gás nitrogênio sua densidade irá aumentar.
  4. Volumes iguais dos gases metano e dióxido de carbono, nas mesmas condições de temperatura e pressão, apresentam as mesmas densidades.
  5. Comprimindo-se um gás a temperatura constante, sua densidade deve diminuir.

Resposta: B

Resolução:

1. A) Incorreta. A Lei de Charles afirma que, a pressão constante, o volume de um gás é diretamente proporcional à sua temperatura absoluta. Ou seja, quanto maior a temperatura, maior o volume do gás.

2. B) Correta. A velocidade média das moléculas de um gás é inversamente proporcional à raiz quadrada da sua massa molar. Como a massa molar do nitrogênio (28 g/mol) é menor que a do oxigênio (32 g/mol), as moléculas de nitrogênio se movem mais rapidamente em comparação com as de oxigênio.

3. C) Incorreta. Ao aquecer um gás ideal à pressão constante, sua densidade diminui. Isso ocorre porque o aumento da temperatura faz com que as moléculas do gás se movam mais rapidamente, ocupando um maior volume.

4. D) Incorreta. A densidade de um gás depende da sua massa molar e do volume que ocupa. Como o metano (CH4) tem menor massa molar que o dióxido de carbono (CO2), volumes iguais dos dois gases nas mesmas condições de temperatura e pressão não apresentarão as mesmas densidades. A densidade do metano será menor.

5. E) Correta. Ao comprimir um gás a temperatura constante, sua densidade aumenta. Isso ocorre porque a compressão diminui o volume do gás, enquanto a massa permanece constante.

02. (ITA) Certa substância gasosa a 0◦C, submetida a uma pressão de 0,333 atm, apresentou uma densidade de 0,656 g.L-1. Sua massa molecular é:

  1. 132
  2. 67
  3. 44
  4. 22
  5. 15

Resposta: C

Resolução:

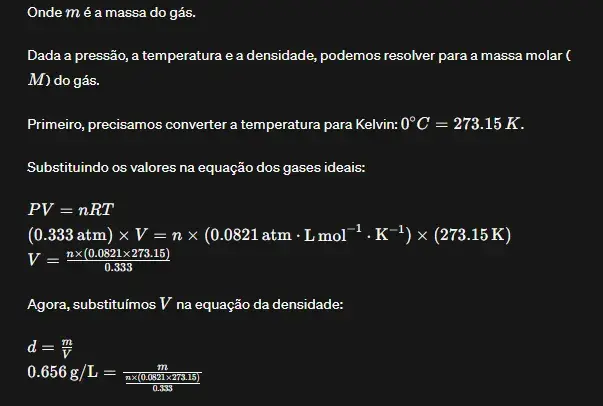
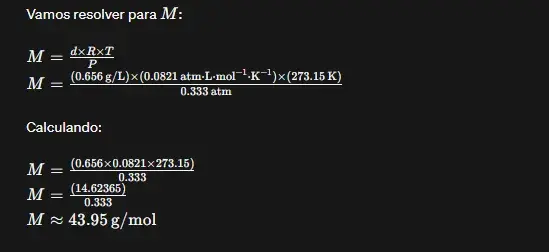
03. (ITA) Temos um frasco contendo um gás à temperatura de 127°C. Querendo expulsar do frasco 1/3 do número de moléculas desse gás, devemos aquecê-lo a:

  1. 42,5°C
  2. 377 K;
  3. 447°C;
  4. 42,5 K;
  5. 600 K.

Resposta: E

Resolução:

04. (IME) Um gás ideal sofre uma expansão isotérmica, seguida de uma compressão adiabática. A variação total da energia interna do gás poderia ser nula se, dentre as opções abaixo, a transformação seguinte for uma

  1. compressão isotérmica
  2. expansão isobárica
  3. compressão isobárica
  4. expansão isocórica
  5. compressão isocórica

Resposta: C

Resolução:

05. (ITA) Uma amostra de 7,5 gramas de um hidrocarboneto ocupa um volume de 5,6 litros nas CNTP, podemos concluir que esse hidrocarboneto corresponde a um:

  1. Alcano
  2. Alceno
  3. Alcino
  4. Ciclano
  5. Cicleno

Resposta: A

Resolução: Para determinar se o hidrocarboneto é um alcano, alceno, alcino, ciclano ou cicleno, precisamos considerar suas propriedades físicas e químicas, bem como o volume que ocupa nas CNTP (Condições Normais de Temperatura e Pressão).

Os alcanos são hidrocarbonetos saturados, ou seja, possuem apenas ligações simples entre os átomos de carbono. Os alcenos são hidrocarbonetos que contêm uma ligação dupla entre dois átomos de carbono, enquanto os alcinos contêm uma ligação tripla entre dois átomos de carbono. Os ciclanos são hidrocarbonetos cíclicos saturados, enquanto os ciclenos são hidrocarbonetos cíclicos insaturados.

A partir da massa molar dos hidrocarbonetos, podemos determinar o número de mols presentes na amostra e, em seguida, determinar o tipo de hidrocarboneto com base na sua estrutura.

Para isso, podemos usar a equação dos gases ideais:

PV=nRT

Onde:

P é a pressão nas CNTP, que é 1 atm

V é o volume em litros, que é 5,6 L

n é o número de mols

R é a constante dos gases ideais, que é 0,0821 L atm / K mol

T é a temperatura em kelvin nas CNTP, que é 273,15 K

Podemos reorganizar a equação para encontrar o número de mols (n):

Podemos reorganizar a equação para encontrar o número de mols (n):

n = PV/RT

n = (1 atm) (5,6 L) / (0,0821 L atm/K mol) (273,15 K)

n ≈ 0,25 mol

Agora, podemos usar a massa molar do hidrocarboneto para determinar seu tipo. Suponhamos que a massa molar média de um hidrocarboneto seja cerca de 30 g/mol (um valor aproximado). Então, a amostra de 7,5 gramas teria cerca de 0,25 mol, o que é compatível com a quantidade de mols que calculamos.

Um hidrocarboneto com uma massa molar tão baixa provavelmente é um alcano ou um alceno, já que estes tendem a ter massas molares menores. Como não podemos determinar com certeza apenas com base na massa molar, precisamos de mais informações sobre a estrutura do hidrocarboneto para distinguir entre alcano e alceno.

Dada a falta de informações adicionais, não podemos determinar com precisão se o hidrocarboneto é um alcano ou alceno. Portanto, a opção mais apropriada seria a letra A, "Alcano", que é o tipo mais comum de hidrocarboneto e tem uma massa molar compatível com os dados fornecidos.

06. (ITA) Considere um gás perfeito monoatômico na temperatura de 0°C, sob uma pressão de 1 atm, ocupando um volume de 56. A velocidade escalar quadrática média das moléculas vale 1840ms–1. Então, a massa do gás

  1. 55g
  2. 100g
  3. 5,0g
  4. 150g
  5. 20g

Resposta: C

Resolução:

07. (ITA) Calcular a massa de gás hélio, contida num balão, sabendo-se que o gás ocupa um volume igual a 5,0 cm3 e está a uma temperatura de - 23°C e a uma pressão de 30 cmHg

  1. 0,186 mg
  2. 0,46 mg
  3. 0,96 mg
  4. 0,186 mg
  5. 0,385 mg

Resposta: E

Resolução:

08. (ITA) Dois balões esféricos de mesmo volume são unidos por um tubo de volume desprezível, provido de torneira. Inicialmente o balão A contém 1,00 mol de gás ideal, e em B há vácuo. Os dois balões são mantidos às temperaturas indicadas no desenho acima. A torneira é aberta durante certo tempo. Voltando a fechá-la, verifica-se que a pressão em B é 0,81 do valor da pressão em A. Quanto do gás deve ter sobrado no balão A?

  1. 0,20 mol
  2. 0,40 mol
  3. 0,50 mol
  4. 0,60 mol
  5. 0,80 mol

Resposta: C

Resolução:

09. (ITA) Para transformar completamente 1cm³ de água a 100°C e 1 atm em vapor (que ocupará 1671cm³) a 100°C e 1 atm, é necessário fornecer 539 calorias. Nestas condições, o trabalho realizado pelo gás em expansão e o aumento da energia interna serão, respectivamente (valores aproximados):

(Dados: 1cal = 4,19 joules; 1 atm = 1,01 . 105 N/m²)

  1. 0,17kJ e 2,09kJ.
  2. 2,09kJ e 0,17kJ.
  3. 0,17kJ e 2,26kJ.
  4. 1,13kJ e 1,13kJ.
  5. Nenhum dos resultados acima.

Resposta: A

Resolução: Para determinar o trabalho realizado pelo gás em expansão e o aumento da energia interna, podemos usar a primeira lei da termodinâmica, que estabelece a conservação da energia em um sistema. A primeira lei da termodinâmica é expressa pela equação:

10. (ITA) Sejam o recipiente (1) , contendo 1 mol de H2 (massa molecular M = 2) e o recipiente (2) contendo 1 mol de He (massa atômica M = 4) ocupando o mesmo volume, ambos mantidos a mesma pressão.

Assinale a alternativa correta:

  1. A temperatura do gás no recipiente 1 é menor que a temperatura do gás no recipiente 2.
  2. A temperatura do gás no recipiente 1 é maior que a temperatura do gás no recipiente 2.
  3. A energia cinética média por molécula do recipiente 1 é maior que a do recipiente 2.
  4. O valor médio da velocidade das moléculas no recipiente 1 é menor que o valor médio da velocidade das moléculas no recipiente 2.
  5. O valor médio da velocidade das moléculas no recipiente 1 é maior que o valor médio da velocidade das moléculas no recipiente 2

Resposta: C e E

Resolução: Para resolver este problema, precisamos entender as relações entre temperatura, massa molecular, energia cinética média e velocidade média das moléculas de um gás.

Temperatura do Gás:

A temperatura de um gás é uma medida da energia cinética média das moléculas. Quanto maior a temperatura, maior a energia cinética média das moléculas.

Energia Cinética Média:

A energia cinética média por molécula de um gás é diretamente proporcional à temperatura. Quanto maior a temperatura, maior a energia cinética média.

Velocidade Média das Moléculas:

A velocidade média das moléculas de um gás é inversamente proporcional à raiz quadrada da massa molar. Quanto maior a massa molar, menor a velocidade média das moléculas.

Dadas essas relações, podemos analisar as afirmações: A) A temperatura do gás no recipiente 1 é menor que a temperatura do gás no recipiente 2.

Incorreto. Ambos os gases estão à mesma temperatura, já que ocupam o mesmo volume e estão à mesma pressão.

B) A temperatura do gás no recipiente 1 é maior que a temperatura do gás no recipiente 2.

Incorreto. Ambos os gases estão à mesma temperatura.

C) A energia cinética média por molécula do recipiente 1 é maior que a do recipiente 2.

Correto. A energia cinética média é diretamente proporcional à temperatura. Portanto, como os gases estão à mesma temperatura, a energia cinética média por molécula é maior no recipiente 1, pois o hidrogênio possui massa molecular menor que o hélio.

D) O valor médio da velocidade das moléculas no recipiente 1 é menor que o valor médio da velocidade das moléculas no recipiente 2.

Incorreto. A velocidade média das moléculas é inversamente proporcional à raiz quadrada da massa molar. Como a massa molar do hélio é maior que a do hidrogênio, a velocidade média das moléculas no recipiente 1 é maior.

E) O valor médio da velocidade das moléculas no recipiente 1 é maior que o valor médio da velocidade das moléculas no recipiente 2.

Correto. Como explicado acima, a massa molar do hidrogênio é menor que a do hélio, o que resulta em uma velocidade média das moléculas maior no recipiente 1.