Matrizes e Determinantes

01. (ITA 2021) Sejam A e B matrizes quadradas de ordem ímpar. Suponha que A é simétrica e que B é antissimétrica. Considere as seguintes afirmações:

I. (A + B)² = A² + 2AB + B².

II. A comuta com qualquer matriz simétrica.

III. B comuta com qualquer matriz antissimétrica.

IV. det (A B) = 0.

É(são) VERDADEIRA(S):

1. nenhuma.
2. apenas I.
3. apenas III.
4. apenas IV.
5. apenas II e IV.

02. (ITA 2021) Seja A uma matriz real quadrada de ordem 2 tal que

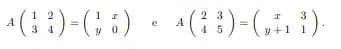
Então, o traço da matriz A é igual a:

1. 0
2. 1
3. 2
4. 3
5. 4

03. (ITA 2019) Considere as seguintes afirmações a respeito de matrizes A de ordem n x n inversíveis, tais que os seus elementos e os de sua inversa sejam todos números inteiros:

I. |det(A)| = 1.

II. A^T = A^-1.

III. A + A^-1 é uma matriz diagonal.

É(são) sempre VERDADEIRA(S)

1. apenas I.
2. apenas III.
3. apenas I e II.
4. apenas I e III.
5. todas.

04. (ITA 2018) Sejam x₁,....x₅ e y₁,....y₅ números reais arbitrários e A = (a_ij) uma matriz 5 x 5 definida por a_ij = x_i + x_j, 1 ≤ i, j ≤ 5. Se r é a característica da matriz A, então o maior valor possível de r é:

1. 1
2. 2
3. 3
4. 4
5. 5

05. (ITA 2018) Sejam A e B matrizes quadradas n×n tais que A+B = A·B e I_n a matriz identidade n×n. Das afirmações:

I. I_n − B é inversível;

II. I_n − A é inversível;

III. A · B = B · A.

é (são) verdadeira(s)

1. Somente I.
2. Somente II.
3. Somente III.
4. Somente I e II.
5. Todas.

06. (ITA 2018) Uma progressão aritmética (a1,a2,...,an) satisfaz a propriedade: para cada n ∈ N, a soma da progressão é igual a 2n² + 5n. Nessas condições, o determinante da matriz é

1. -96
2. -85
3. 63
4. 99
5. 115

07. (ITA 2018) Considere a matriz

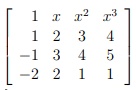
x ∈ R. Se o polinômio p(x) é dado por p(x) = detA, então o produto das raízes de p(x) é

1. $\frac{1}{2}$
2. $\frac{1}{3}$
3. $\frac{1}{5}$
4. $\frac{1}{7}$
5. $\frac{1}{\mathrm{11}}$

08. (ITA 2017)

Considere A = P ⁻¹DP. O valor de det(A² + A) é

1. 144.
2. 180.
3. 240.
4. 324.
5. 360.

09. (IME 2017)

Seja

com a ε R . Sabe-se que det(A² - 2A + ℓ = 16). A soma dos valores de a que satisfazem essa condição é:

1. 0
2. 1
3. 2
4. 3
5. 4

10. (ITA 2016)

Se M

11. (IME 2015) Seja O maior valor de a, com a≠1, que satisfaz A²⁴ = I é:

1. $\frac{1}{2}$
2. $\frac{\mathrm{\surd 2}}{2}$
3. $\frac{\mathrm{\surd 3}}{2}$
4. $\frac{\mathrm{\surd 2}}{4}$$\left(\sqrt{3-1}\right)$
5. $\frac{\mathrm{\surd 2}}{4}$$\left(\sqrt{31}\right)\frac{\sqrt{2}}{4}\left(\sqrt{3}1\right)$

12. (ITA 2015) Considere a matriz M = (mij )2×2 tal que mij = j − i + 1, i, j = 1, 2. Sabendo-se que então o valor de n é igual a

1. 4.
2. 5.
3. 6.
4. 7.
5. 8.

13. (IME 2014) Dada a matriz A, a soma do módulo dos valores de x que tornam o determinante da matriz A nulo é:

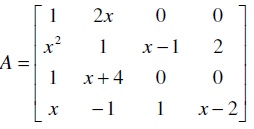
1. 7
2. 8
3. 9
4. 10
5. 11

14. (ITA 2014) Considere as seguintes afirmações sobre as matrizes quadradas A e B de ordem n, com A inversível e B antissimétrica:

I. Se o produto AB for inversível, então n é par;

II. Se o produto AB não for inversível, então n é ímpar;

III. Se B for inversível, então n é par.

Destas afirmações, é (são) verdadeira(s)

1. apenas I.
2. apenas I e II.
3. apenas I e III.
4. apenas II e III.
5. todas.

15. (ITA 2014) Seja M uma matriz quadrada de ordem 3, inversível, que satisfaz a igualdade

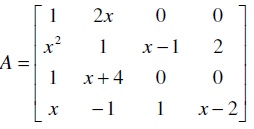
Então, um valor possível para o determinante da inversa de M é

1. $\frac{1}{3}$
2. $\frac{1}{2}$
3. $\frac{2}{3}$
4. $\frac{4}{5}$
5. $\frac{5}{4}$

16. (ITA 2014) Considere a equação A(t)X = B(t), t ∈ R, em que

Sabendo que det A(t) = 1 e t ≠ 0, os valores de x, y e z são, respectivamente,

1. 2 √2, 0, −3√2.
2. − 2√2, 0, −3√2.
3. 0, 3√2, 2√2.
4. 0, 2√3, √3.
5. 2 √3, − √3, 0.