Geometria Espacial

1. (ITA 2019) A superfície lateral de um cone circular reto corresponde a um setor circular de 216°, quando planificada. Se a geratriz do cone mede 10 cm, então a medida de sua altura, em cm, é igual a

1. 5.
2. 6.
3. 7.
4. 8.
5. 9.

2. (ITA 2019) Os volumes de um tronco de cone, de uma esfera de raio 5 cm e de um cilindro de altura 11 cm formam nessa ordem uma progressão aritmética. O tronco de cone é obtido por rotação de um trapézio retângulo, de altura 4 cm e bases medindo 5 cm e 9 cm, em torno de uma reta passando pelo lado de menor medida. Então, o raio da base do cilindro é, em cm, igual a

1. 2√2
2. 2√3
3. 4
4. 2√5
5. 2√6

3. (ITA 2018) Considere a classicação: dois vértices de um paralelepípedo são não adjacentes quando não pertencem à mesma aresta. Um tetraedro é formado por vértices não adjacentes de um paralelepípedo de arestas 3 cm, 4 cm e 5 cm. Se o tetraedro tem suas arestas opostas de mesmo comprimento, então o volume do tetraedro é, em cm³:

1. 10
2. 12
3. 15
4. 20
5. 30

4. (IME 2017) Um prisma retangular reto possui três arestas que formam uma progressão geométrica de razão 2. Sua área total é de 28cm².

Calcule o valor da diagonal do referido prisma.

1. √17 cm
2. √19 cm
3. √21 cm
4. 2√7 cm
5. √29 cm

5. (ITA 2017) Considere a reta r: y = 2x. Seja A = (3, 3) o vértice de um quadrado ABCD, cuja diagonal BD está contida em r. A área deste quadrado é

1. $\frac{9}{5}$
2. $\frac{12}{5}$
3. $\frac{18}{5}$
4. $\frac{21}{5}$
5. $\frac{24}{5}$

6. (IME 2016) Um tronco de pirâmide regular possui 12 vértices. A soma dos perímetros das bases é 36 cm, a soma das áreas das bases é 30√3 cm2 e sua altura mede 3 cm. Calcule o volume do tronco de pirâmide.

1. 50cm³
2. 42 $\frac{\mathrm{\surd 3}}{3}$cm³
3. 43 $\frac{\mathrm{\surd 3}}{2}$cm³
4. 43√2cm³
5. 42√3cm³

7. (ITA 2016) Uma esfera S1, de raio R > 0, está inscrita num cone circular reto K. Outra esfera, S2, de raio r, com 0 < r < R, está contida no interior de K e é simultaneamente tangente à esfera S1 e à superfície lateral de K. O volume de K é igual a

1. $\frac{{\mathrm{\pi R}}^5}{\mathrm{3r(R\; -\; r)}}$
2. $\frac{{\mathrm{2\pi R}}^5}{\mathrm{3r(R\; -\; r)}}$
3. $\frac{{\mathrm{\pi R}}^5}{\mathrm{r(R\; -\; r)}}$
4. $\frac{{\mathrm{4\pi R}}^5}{\mathrm{3r(R\; -\; r)}}$
5. $\frac{{\mathrm{5\pi R}}^5}{\mathrm{3r(R\; -\; r)}}$

8. (ITA 2015) Uma taça em forma de cone circular reto contém um certo volume de um líquido cuja superfície dista h do vértice do cone. Adicionando-se um volume idêntico de líquido na taça, a superfície do líquido, em relação à original, subirá de

1. $\sqrt[3]{2}-h$
2. $\sqrt[3]{2}-1$
3. ($\sqrt[3]{2}-1$)
4. h
5. $\frac{\mathrm{h}}{2}$

9. (ITA 2014) Considere o sólido de revolução obtido pela rotação de um triângulo isósceles ABC em torno de uma reta paralela à base BC que dista 0, 25 cm do vértice A e 0, 75 cm da base BC. Se o lado AB mede $\sqrt{\frac{{\pi }^2+1}{2\pi }}$, o volume desse sólido, em cm³, é igual a

1. $\frac{9}{16}$
2. $\frac{13}{96}$
3. $\frac{7}{24}$
4. $\frac{9}{24}$
5. $\frac{11}{96}$

10. (IME 2014) Em um prisma oblíquo ABCDEFA’B’C’D’E’F’, cuja base ABCDEF é um hexágono regular de lado &, a face lateral EFF’E’ está inclinada 45° em relação à base, e a projeção ortogonal da aresta F’E’ sobre a base ABCDEF coincide com a aresta BC. O volume do prisma é:

1. $\frac{3\sqrt{3}}{2}{a}^3$
2. $\frac{9}{4}{a}^3$
3. $\frac{5\sqrt{3}}{3}{a}^3$
4. $\frac{9}{2}{a}^3$
5. $\frac{5}{2}{a}^3$

11. (IME 2013) Seja SABCD uma pirâmide, cuja base é um quadrilátero convexo ABCD. A aresta SD é a altura da pirâmide. Sabe-se que

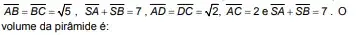
1. √5
2. √7
3. √11
4. √13
5. √17

12. (ITA 2012) Um cone circular reto de altura 1 cm e geratriz $\frac{2\sqrt{3}}{3}$ cm é interceptado por um plano paralelo à sua base, sendo determinado, assim, um novo cone. Para que este novo cone tenha o mesmo volume de um cubo de aresta ${\left(\frac{\mathrm{\pi \; <!--\; greek\; small\; letter\; pi\; -->}}{243}\right)}^{1/3}$ cm, é necessário que a distância do plano à base do cone original seja, em cm, igual a

1. $\frac{1}{4}$
2. $\frac{1}{3}$
3. $\frac{1}{2}$
4. $\frac{2}{3}$
5. $\frac{3}{4}$

13. (ITA 2012) A superfície lateral de um cone circular reto é um setor circular de 120° e área igual a 3π cm². A área total e o volume deste cone medem, em cm² e cm³, respectivamente

1. 4π e $\frac{2\mathrm{\pi \; <!--\; greek\; small\; letter\; pi\; -->}\sqrt{2}}{3}$
2. 4π e $\frac{\mathrm{\pi \; <!--\; greek\; small\; letter\; pi\; -->}\sqrt{2}}{3}$
3. 4π e π $\sqrt{2}$
4. 3π e $\frac{2\mathrm{\pi \; <!--\; greek\; small\; letter\; pi\; -->}\sqrt{2}}{3}$
5. π e 2π $\sqrt{2}$

14. (ITA 2011) Considere as afirmações:

I − Existe um triedro cujas 3 faces têm a mesma medida a = 120°.

II − Existe um ângulo poliédrico convexo cujas faces medem, respectivamente, 30°, 45°, 50°, 50° e 170°.

III − Um poliedro convexo que tem 3 faces triangulares, 1 face quadrangular, 1 face pentagonal e 2 faces hexagonais tem 9 vértices.

IV − A soma das medidas de todas as faces de um poliedro convexo com 10 vértices é 2880°.

Destas, é(são) correta(s) apenas

1. II.
2. IV.
3. II e IV.
4. I, II e IV.
5. II, III e IV.

15. (ITA 2010) Um cilindro reto de altura $\frac{\mathrm{\surd 6}}{3}$ cm está inscrito num tetraedro regular e tem sua base em uma das faces do tetraedro. Se as arestas do tetraedro medem 3 cm; o volume do cilindro, em cm³, é igual a

1. $\frac{\mathrm{\pi \; <!--\; greek\; small\; letter\; pi\; -->}\sqrt{3}}{4}$
2. $\frac{\mathrm{\pi \; <!--\; greek\; small\; letter\; pi\; -->}\sqrt{3}}{6}$
3. $\frac{\mathrm{\pi \; <!--\; greek\; small\; letter\; pi\; -->}\sqrt{6}}{6}$
4. $\frac{\mathrm{\pi \; <!--\; greek\; small\; letter\; pi\; -->}\sqrt{6}}{9}$
5. $\frac{\mathrm{\pi \; <!--\; greek\; small\; letter\; pi\; -->}}{3}$

16. (ITA 2011) Uma esfera está inscrita em uma pirâmide regular hexagonal cuja altura mede 12 cm e a aresta da base mede $\frac{\mathrm{10}}{3}$ √3 cm. Então o raio da esfera, em cm, é igual a

1. $\frac{10}{3}$ √3
2. $\frac{\mathrm{13}}{3}$
3. $\frac{\mathrm{15}}{4}$
4. 2√3
5. $\frac{\mathrm{10}}{3}$

17. (ITA 2009) Uma esfera é colocada no interior de um cone circular reto de 8 cm de altura e de 60° de ângulo de vértice. Os pontos de contato da esfera com a superfície lateral do cone definem uma circunferência e distância 2√3 cm do vértice do cone. O volume do cone não ocupado pela esfera, em cm³.

1. $\frac{\mathrm{416}}{9}$π
2. $\frac{\mathrm{480}}{9}$π
3. $\frac{\mathrm{500}}{9}$π
4. $\frac{\mathrm{512}}{9}$π
5. $\frac{\mathrm{542}}{9}$π

18. (ITA 2009) Os pontos A = (3; 4) e B = (4; 3) s]ao vértices de um cubo, em que AB é uma das arestas. A área lateral do octaedro cujos vértices são os pontos médios da face do cubo é igual a

1. √8
2. 3
3. √12
4. 4
5. √18

19. (ITA 2008) Um diedro mede 120°. A distância da aresta do diedro ao centro de uma esfera de volume 4√3πcm³ que tangencia as faces do diedro é, em cm, igual a

1. 3√3
2. 3√2
3. 2√3
4. 2√2
5. 2

20. (ITA) Cortando-se uma pirâmide regular de altura h, com um plano paralelo à base, resulta uma segunda pirâmide. Se a razão entre as áreas das superfícies laterais das pirâmides (menor/maior) for r, a que distância do vértice deve passar o plano?

1. $h^{2}r$
2. $h\sqrt{r}$
3. $r\sqrt{h}$
4. $\frac{\sqrt{r}}{h}$
5. hr

21. (ITA) Cortando-se um determinado prisma triangular, reto, por um plano α que forma um ângulo de 45^o com o plano da base ABC observamos que a reta r, interseção de α com o plano da base, dista 7 cm de A, 5 cm de B e 2 cm de C. Se a área da base for 21 cm², o volume do tronco de prisma compreendido entre a base ABC e o plano α será:

1. 105 cm³
2. 294 cm³
3. 98 cm³
4. $98\sqrt{2}{\mathrm{cm}}^3$
5. $\frac{98}{\sqrt{2}}{\mathrm{cm}}^3$

22. (ITA) As medidas dos catetos de um triângulo retângulo são (sen x) cm e (cos x) cm. Um estudante calculou o volume do sólido gerado pela rotação deste triângulo em torno da hipotenusa, e obteve como resultado π cm³. Considerando este resultado como certo, podemos afirmar que:

1. $x=\frac{\mathrm{\pi }}{6}$
2. $x=\frac{\mathrm{\pi }}{3}$
3. $x=\frac{\mathrm{\pi }}{4}$
4. $x=\frac{\mathrm{\pi }}{5}$
5. N.D.R.A.

23. (ITA) Um poliedro convexo tem exatamente 6 vértices e exatamente 12 arestas.

Considere as afirmativas:

I – O número de faces é igual a 8;

II – O número de faces quadrangulares é igual ao número de faces triangulares;

III – Todas as faces do poliedro são triangulares;
IV – Todas as faces do poliedro são quadrangulares;

Assinale a alternativa correta.

1. Somente a afirmativa I é correta.
2. Somente as afirmativas I e II são corretas.
3. Somente as afirmativas I e III são corretas.
4. Somente as afirmativas I e IV são corretas.
5. Todas as afirmativas estão erradas.