Análise Combinatória e Probabilidade
Lista de 09 exercícios de Matemática com gabarito sobre o tema Análise Combinatória e Probabilidade com questões do ITA/IME.
1. (ITA) Quantos anagramas com 4 letras distintas podemos formar com as 10 primeiras letras do alfabeto e que contenham 2 das letras a, b, c ?
- 1692
- 1572
- 1520
- 1512
- 1392
2. (ITA) Uma escola oferece 5 diferentes classes de línguas, 4 diferentes classes de ciências e 3 diferentes classes de matemática. De quantas maneiras é possível escolher 2 classes, não ambas do mesmo assunto?
- 64
- 50
- 21
- 36
- 47
3. (ITA) Reduzidos os termos semelhantes, quantos termos existem no desenvolvimento de (a + b + c + d + e)17?
- C21,5
- C17,5
- C12,5
- 2.C21,5
- 2.C17,5
4. (ITA) Se colocarmos em ordem crescente todos os números de 5 algarismos distintos obtidos com 1, 3, 4, 6 e 7, a posição do número 61473 é:
- 76º
- 78º
- 80º
- 82º
- 84º
5. (ITA 2018) São dadas duas caixas, uma delas contém três bolas brancas e duas pretas e a outra contém duas bolas brancas e uma preta. Retira-se, ao acaso, uma bola de cada caixa. Se P1 é a probabilidade de que pelo menos uma bola seja preta e P2 a probabilidade de as duas bolas serem da mesma cor, então P1 + P2 vale
- 1
6. (ITA) Considere os números de 2 a 6 algarismos distintos formados utilizando-se apenas 1, 2, 4, 5, 7 e 8. Quantos destes números são ímpares e começam com um dígito par?
- 375
- 465
- 545
- 585
- 625
07. (IME 2016) Um hexágono é dividido em 6 triângulos equiláteros. De quantas formas podemos colocar os números de 1 a 6 em cada triângulo, sem repetição, de maneira que a soma dos números em três triângulos adjacentes seja sempre múltiplo de 3? Soluções obtidas por rotação ou reflexão são diferentes, portanto as figuras abaixo mostram duas soluções distintas.
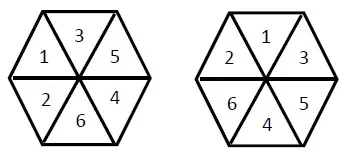
- 12
- 24
- 36
- 48
- 96
08. (ITA 2016) Pintam-se N cubos iguais utilizando-se 6 cores diferentes, uma para cada face. Considerando que cada cubo pode ser perfeitamente distinguido dos demais, o maior valor possível de N é igual a
- 10
- 15
- 20
- 25
- 30
09. (IME 2013) Sabe-se que o valor do sexto termo da expansão em binômio de Newton de
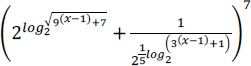
é 84. O valor da soma dos possíveis valores de 0 é
- 1
- 2
- 3
- 4
- 5