Simulado de Matemática

01. (Fuvest 2021)

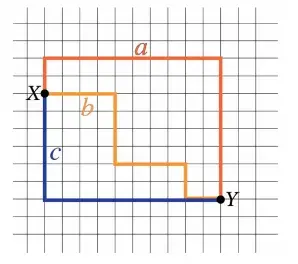
A figura ilustra graficamente uma região de um bairro, com ruas ortogonais entre si. O ponto X indica um condomínio residencial, e o ponto Y indica a entrada de um parque. Três moradores realizam caminhos diferentes para chegar ao ponto Y, partindo do ponto X, ilustrados com cores diferentes.

Se a, b e c representam as distâncias percorridas por esses moradores nesses caminhos, é correto afirmar que

1. a = b = c.
2. b = c < a.
3. c < b < a.
4. b < c = a.
5. c < a = b.

02. (Fuvest 2020) A dona de uma lanchonete observou que, vendendo um combo a R$ 10,00, 200 deles são vendidos por dia, e que, para cada redução de R$ 1,00 nesse preço, ela vende 100 combos a mais.

Nessas condições, qual é a máxima arrecadação diária que ela espera obter com a venda desse combo?

1. R$ 2.000,00
2. R$ 3.200,00
3. R$ 3.600,00
4. R$ 4.000,00
5. R$ 4.800,00

03. (Fuvest 2019) Em uma família, o número de irmãs de cada filha é igual à metade do número de irmãos. Cada filho tem o mesmo número de irmãos e irmãs.

O número total de filhos e filhas da família é

1. 4
2. 5
3. 7
4. 10
5. 15

04. (Fuvest 2018) Dentre os candidatos que fizeram provas de matemática, português e inglês num concurso, 20 obtiveram nota mínima para aprovação nas três disciplinas. Além disso, sabe-se que:

I. 14 não obtiveram nota mínima em matemática;

II. 16 não obtiveram nota mínima em português;

III. 12 não obtiveram nota mínima em inglês;

IV. 5 não obtiveram nota mínima em matemática e em português;

V. 3 não obtiveram nota mínima em matemática e em inglês;

VI. 7 não obtiveram nota mínima em português e em inglês e

VII. 2 não obtiveram nota mínima em português, matemática e inglês.

A quantidade de candidatos que participaram do concurso foi

1. 44
2. 46
3. 47
4. 48
5. 49

05. (Fuvest 2017) Sejam a e b dois números inteiros positivos. Diz-se que a e b são equivalentes se a soma dos divisores positivos de a coincide com a soma dos divisores positivos de b. Constituem dois inteiros positivos equivalentes:

1. 8 e 9.
2. 9 e 11.
3. 10 e 12.
4. 15 e 20.
5. 16 e 25

06. (Fuvest 2021) O quadrinho aborda o tema de números primos, sobre os quais é correto afirmar:

1. Todos os números primos são ímpares.
2. Existem, no máximo, 7 trilhões de números primos.
3. Todo número da forma 2ⁿ + 1,n ∈ ℕ, é primo.
4. Entre 24 e 36, existem somente 2 números primos.
5. O número do quadrinho, 143, é um número primo.

07. (Fuvest 2020) Carros que saem da cidade A rumo a alguma das cidades turísticas E, F e G fazem caminhos diversos, passando por pelo menos uma das cidades B, C e D, apenas no sentido indicado pelas setas, como mostra a figura. Os números indicados nas setas são as probabilidades, dentre esses carros, de se ir de uma cidade a outra.

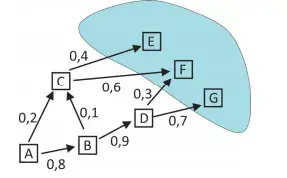
Nesse cenário, a probabilidade de um carro ir de A a F é

1. 0,120.
2. 0,216.
3. 0,264.
4. 0,336.
5. 0,384.

08. (Fuvest 2019) Forma‐se uma pilha de folhas de papel, em que cada folha tem 0,1 mm de espessura. A pilha é formada da seguinte maneira: coloca‐se uma folha na primeira vez e, em cada uma das vezes seguintes, tantas quantas já houverem sido colocadas anteriormente. Depois de 33 dessas operações, a altura da pilha terá a ordem de grandeza

1. da altura de um poste.
2. da altura de um prédio de 30 andares.
3. do comprimento da Av. Paulista.
4. da distância da cidade de São Paulo (SP) à cidade do Rio de Janeiro (RJ).
5. do diâmetro da Terra.

09. (Fuvest 2018) Em uma urna, há bolas amarelas, brancas e vermelhas. Sabe- se que:

I. A probabilidade de retirar uma bola vermelha dessa urna é o dobro da probabilidade de retirar uma bola amarela.

II. Se forem retiradas 4 bolas amarelas dessa urna, a probabilidade de retirar uma bola vermelha passa a ser 1/2.

III. Se forem retiradas 12 bolas vermelhas dessa urna, a probabilidade de retirar uma bola branca passa a ser 1/2.

A quantidade de bolas brancas na urna é

1. 8
2. 10
3. 12
4. 14
5. 16

10. (Fuvest 2017) Cláudia, Paulo, Rodrigo e Ana brincam entre si de amigo-secreto (ou amigo-oculto). Cada nome é escrito em um pedaço de papel, que é colocado em uma urna, e cada participante retira um deles ao acaso. A probabilidade de que nenhum participante retire seu próprio nome é

1. 1/4
2. 7/24
3. 1/3
4. 3/8
5. 5/12

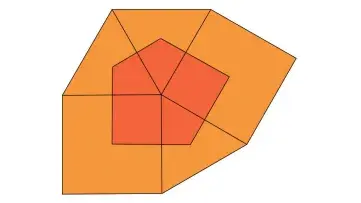
11. (Fuvest 2021) Três triângulos equiláteros e dois quadrados formam uma figura plana, como ilustrado. Seus centros são os vértices de um pentágono irregular, que está destacado na figura.

Se T é a área de cada um dos triângulos e Q a área de cada um dos quadrados, a área desse pentágono é

1. T + Q.
2. 1/2 T + 1/2 Q.
3. T + 1/2 Q.
4. 1/3 T + 1/4 Q.
5. 1/3 T + 1/2 Q.

12. (Fuvest 2020) Se, em 15 anos, o salário mínimo teve um aumento nominal de 300% e a inflação foi de 100%, é correto afirmar que o aumento real do salário mínimo, nesse período, foi de

1. 50%.
2. 100%.
3. 150%.
4. 200%.
5. 250%.

13. (Fuvest 2019) Uma empresa estuda cobrir um vão entre dois prédios (com formato de paralelepípedos reto‐retângulos) que têm paredes laterais paralelas, instalando uma lona na forma de um quadrilátero, com pontas presas nos pontos A, B, C e D, conforme indicação da figura.

Sabendo que a lateral de um prédio tem 80 m de altura e 28 m de largura, que a lateral do outro prédio tem 60 m de altura e 20 m de largura e que essas duas paredes laterais distam 15 m uma da outra, a área total dessa lona seria de

1. 300 m²
2. 360 m²
3. 600 m²
4. 720 m²
5. 1.200 m²

14. (Fuvest 2018) Maria quer comprar uma TV que está sendo vendida por R$ 1.500,00 à vista ou em 3 parcelas mensais sem juros de R$ 500,00. O dinheiro que Maria reservou para essa compra não é suficiente para pagar à vista, mas descobriu que o banco oferece uma aplicação financeira que rende 1% ao mês. Após fazer os cálculos, Maria concluiu que, se pagar a primeira parcela e, no mesmo dia, aplicar a quantia restante, conseguirá pagar as duas parcelas que faltam sem ter que colocar nemtirar um centavo sequer. Quanto Maria reservou para essa compra, em reais?

1. 1.450,20
2. 1.480,20
3. 1.485,20
4. 1.495,20
5. 1.490,20

15. (Fuvest 2017) Considere as funções f(x) = x² + 4 e g(x) = 1 + log 1/2 x, em que o domínio de f é o conjunto dos números reais e o domínio de g é o conjunto dos números reais maiores do que 0. Seja

h(x) = 3f(g(x)) + 2g(f(x)),

em que x > 0. Então, h(2) é igual a

1. 4
2. 8
3. 12
4. 16
5. 20

16. (Fuvest 2021) Um comerciante adotou como forma de pagamento uma máquina de cartões, cuja operadora cobra uma taxa de 6% em cada venda. Para continuar recebendo exatamente o mesmo valor por cada produto, ele resolveu aplicar um reajuste nos preços de todos os produtos da loja.

Se P era o valor de uma mercadoria antes da adoção da máquina, o novo valor V deve ser calculado por

1. V = P + 0,06
2. V = 0,94 · 1,06 · P
3. V = 1,6 · P
4. V = P/0,94
5. V = 0,94 · P

17. (Fuvest 2020) O cilindro de papelão central de uma fita crepe tem raio externo de 3 cm. A fita tem espessura de 0,01 cm e dá 100 voltas completas.

Considerando que, a cada volta, o raio externo do rolo é aumentado no valor da espessura da fita, o comprimento total da fita é de, aproximadamente,

Note e adote:

π ≅ 3,14.

1. 9,4 m.
2. 11,0 m.
3. 18,8 m.
4. 22,0 m.
5. 25,1 m.

18. (Fuvest 2019) Considere a função polinomial f: R → R definida por

f(x) = ax² + bx + c

em que a, b, c ∈ R e a ≠ 0. No plano cartesiano xy, a única intersecção da reta y = 2 com o gráfico de f é o ponto (2; 2) e a intersecção da reta x = 0 com o gráfico de f é o ponto ( 0; -6), O valor de a + b + c é

1. -2
2. 0
3. 2
4. 4
5. 6

19. (Fuvest 2018) Doze pontos são assinalados sobre quatro segmentos de reta de forma que três pontos sobre três segmentos distintos nunca são colineares, como na figura.

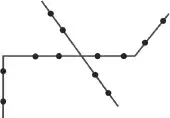
O número de triângulos distintos que podem ser desenhados com os vértices nos pontos assinalados é

1. 200
2. 204
3. 208
4. 212
5. 220

20. (Fuvest 2017) O polinômio P(x) = x³ – 3x² + 7x – 5 possui uma raiz complexa ξ cuja parte imaginária é positiva. A parte real de ξ 3 é igual a

1. -11
2. -7
3. 9
4. 10
5. 12