Resolução: PA/PG

1. (Enem 2020) No Brasil, o tempo necessário para um estudante realizar sua formação até a diplomação em um curso superior, considerando os 9 anos de ensino fundamental, os 3 anos do ensino médio e os 4 anos de graduação (tempo médio), é de 16 anos. No entanto, a realidade dos brasileiros mostra que o tempo médio de estudo de pessoas acima de 14 anos é ainda muito pequeno, conforme apresentado na tabela

Considere que o incremento no tempo de estudo, a cada período, para essas pessoas, se mantenha constante até o ano 2050, e que se pretenda chegar ao patamar de 70% do tempo necessário à obtenção do curso superior dado anteriormente.

1. 2018.
2. 2023.
3. 2031.
4. 2035.
5. 2043.

2. (Enem 2020) O artista gráfico holandês Maurits Cornelius Escher criou belíssimas obras nas quais as imagens se repetiam, com diferentes tamanhos, induzindo ao raciocínio de repetição infinita das imagens. Inspirado por ele, um artista fez um rascunho de uma obra na qual propunha a ideia de construção de uma sequência de infinitos quadrados, cada vez menores, uns sob os outros, conforme indicado na figura.

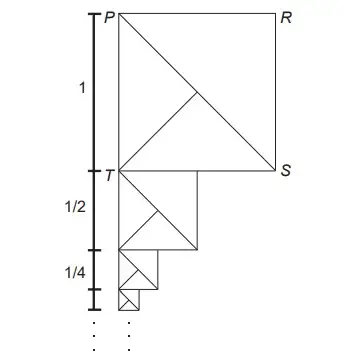
O quadrado PRST, com lado de medida 1, é o ponto de partida. O segundo quadrado é construído sob ele tomando-se o ponto médio da base do quadrado anterior e criando-se um novo quadrado, cujo lado corresponde à metade dessa base. Essa sequência de construção se repete recursivamente.

Qual é a medida do lado do centésimo quadrado construído de acordo com esse padrão?

1. ${\left(\frac{1}{2}\right)}^{100}$
2. ${\left(\frac{1}{2}\right)}^{99}$
3. ${\left(\frac{1}{2}\right)}^{97}$
4. ${\left(\frac{1}{2}\right)}^{-98}$
5. ${\left(\frac{1}{2}\right)}^{-99}$

03. (Enem 2018) A raiva é uma doença viral e infecciosa, transmitida por mamíferos. A campanha nacional de vacinação antirrábica tem o objetivo de controlar a circulação do vírus da raiva canina e felina, prevenindo a raiva humana. O gráfico mostra a cobertura (porcentagem de vacinados) da campanha, em cães, nos anos de 2013, 2015 e 2017, no município de Belo Horizonte, em Minas Gerais. Os valores das coberturas dos anos de 2014 e 2016 não estão informados no gráfico e deseja-se estimá-los.

Para tal, levou-se em consideração que a variação na cobertura de vacinação da campanha antirrábica, nos períodos de 2013 a 2015 e de 2015 a 2017, deu-se de forma linear

Qual teria sido a cobertura dessa campanha no ano de 2014?

1. 62,3%
2. 63,0%
3. 63,5%
4. 64,0%
5. 65,5%

04. (Enem 2018) A prefeitura de um pequeno município do interior decide colocar postes para iluminação ao longa de uma estrada retilínea, que inicia em uma praça central e termina numa fazenda na zona rural. Como a praça já possui iluminação, o primeiro poste será colocado a 80 metros da praça, o segundo, a 100 metros, o terceiro, a 120 metros, e a assim sucessivamente, mantendo-se sempre uma distância de vinte metros entre os postes, até que o último poste seja colocado a uma distância de 1 380 metros da praça.

Se a prefeitura pode pagar, no máximo, R$ 8 000,00 por poste colocado, o maior valor que poderá gastar com a colocação desses postes é

1. R$ 512 000, 00
2. R$ 520 000, 00
3. R$ 528 000, 00
4. R$ 552 000, 00
5. R$ 584 000, 00

05. (Enem PPL 2016) Com o objetivo de trabalhar a concentração e a sincronia de movimentos dos alunos de uma de suas turmas, um professor de educação física dividiu essa turma em três grupos (A, B e C) e estipulou a seguinte atividade: os alunos do grupo A deveriam bater palmas a cada 2 s, os alunos do grupo B deveriam bater palmas a cada 3 s e os alunos do grupo C deveriam bater palmas a cada 4 s.

O professor zerou o cronômetro e os três grupos começaram a bater palmas quando ele registrou 1 s. Os movimentos prosseguiram até o cronômetro registrar 60 s.

Um estagiário anotou no papel a sequência formada pelos instantes em que os três grupos bateram palmas simultaneamente.

Qual é o termo geral da sequência anotada?

1. 12 n, com n um número natural, tal que 1 ≤ n ≤ 5.
2. 24 n, com n um número natural, tal que 1 ≤ n ≤ 2.
3. 12 (n - 1 ), com n um número natural, tal que 1 ≤ n ≤ 6.
4. 12 (n - 1 ) + 1 , com n um número natural, tal que 1 ≤ n ≤ 5.
5. 24 (n - 1 ) + 1 , com n um número natural, tal que 1 ≤ n ≤ 3.

06. (Enem PPL 2017) Os consumidores X, Y e Z desejam trocar seus planos de internet móvel na tentativa de obterem um serviço de melhor qualidade. Após pesquisarem, escolheram uma operadora que oferece cinco planos para diferentes perfis, conforme apresentado no quadro.

Em cada plano, o consumidor paga um valor fixo(preço mensal da assinatura) pela franquia contratada e um valor variável, que depende da quantidade de MB utilizado além da franquia. Considere que a velocidade máxima de acesso seja a mesma, independentemente do plano, que os consumos mensais de X, Y e Z são de 190 MB, 450 MB e 890 MB, respectivamente, e que cada um deles escolherá apenas um plano.

Com base nos dados do quadro, as escolhas dos planos com menores custos para os consumidores X, Y e Z, respectivamente, são

1. A, C e C
2. A, B e D.
3. B, B e D.
4. B, C e C
5. B, C e D.

07. (Enem 2016) Para comemorar o aniversário de uma cidade, a prefeitura organiza quatro dias consecutivos de atrações culturais. A experiência de anos anteriores mostra que, de um dia para o outro, o número de visitantes no evento é triplicado. É esperada a presença de 345 visitantes para o primeiro dia do evento.

Uma representação possível do número esperado de participantes para o último dia é

1. 3 x 345
2. (3 + 3 + 3) x 345
3. 3³ x 345
4. 3 x 4 x 345
5. 3⁴ x 345

08. (Enem 2015) Um casal realiza um financiamento imobiliário de R$ 180 000,00, a ser pago em 360 prestações mensais, com taxa de juros efetiva de 1% ao mês. A primeira prestação é paga um mês após a liberação dos recursos e o valor da prestação mensal é de R$ 500,00 mais juro de 1% sobre o saldo devedor (valor devido antes do pagamento). Observe que, a cada pagamento, o saldo devedor se reduz em R$ 500,00 e considere que não há prestação em atraso.

Efetuando o pagamento dessa forma, o valor, em reais, a ser pago ao banco na décima prestação é de

1. 2 075,00.
2. 2 093,00.
3. 2 138,00.
4. 2 255,00.
5. 2 300,00.

09. (Enem PPL 2013) Para um principiante em corrida, foi estipulado o seguinte plano de treinamento diário: correr 300 metros no primeiro dia e aumentar 200 metros por dia, a partir do segundo. Para contabilizar seu rendimento, ele utilizará um chip, preso ao seu tênis, para medir a distância percorrida nos treinos. Considere que esse chip armazene, em sua memória, no máximo 9,5 km de corrida/caminhada, devendo ser colocado no momento do início do treino e descartado após esgotar o espaço para reserva de dados.

Se esse atleta utilizar o chip desde o primeiro dia de treinamento, por quantos dias consecutivos esse chip poderá armazenar a quilometragem desse plano de treino diário?

1. 7
2. 8
3. 9
4. 12
5. 13

10. (Enem 2013) O ciclo de atividade magnética do Sol tem um período de 11 anos. O início do primeiro ciclo registrado se deu no começo de 1755 e se estendeu até o final de 1765. Desde então, todos os ciclos de atividade magnética do Sol têm sido registrados.

Disponível em: http://g1.globo.com. Acesso em: 27 fev. 2013.

No ano de 2101, o Sol estará no ciclo de atividade magnética de número

1. 32
2. 34
3. 33
4. 35
5. 31

11. (Enem 2012) Num projeto da parte elétrica de um edifício residencial a ser construído, consta que as tomadas deverão ser colocadas a 0,20 m acima do piso, enquanto os interruptores de luz deverão ser colocados a 1,47 m acima do piso. Um cadeirante, potencial comprador de um apartamento desse edifício, ao ver tais medidas, alerta para o fato de que elas não contemplarão suas necessidades. Os referenciais de alturas (em metros) para atividades que não exigem o uso de força são mostrados na figura seguinte.

Uma proposta substitutiva, relativa às alturas de tomadas e interruptores, respectivamente, que atenderá àquele potencial comprador é

1. 0,20 m e 1,45 m.
2. 0,20 m e 1,40 m.
3. 0,25 m e 1,35 m.
4. 0,25 m e 1,30 m.
5. 0,45 m e 1,20 m.

12. (Enem 2012) Jogar baralho é uma atividade que estimula o raciocínio. Um jogo tradicional é a Paciência, que utiliza 52 cartas. Inicialmente são formadas sete colunas com as cartas. A primeira coluna tem uma carta, a segunda tem duas cartas, a terceira tem três cartas, a quarta tem quatro cartas, e assim sucessivamente até a sétima coluna, a qual tem sete cartas, e o que sobra forma o monte, que são as cartas não utilizadas nas colunas.

A quantidade de cartas que forma o monte é

1. 21.
2. 24.
3. 26.
4. 28.
5. 31.

13. (Enem 2012) Um maquinista de trem ganha R$ 100,00 por viagem e só pode viajar a cada 4 dias. Ele ganha somente se fizer a viagem e sabe que estará de férias de 1º a 10 de junho, quando não poderá viajar. Sua primeira viagem ocorreu no dia primeiro de janeiro. Considere que o ano tem 365 dias.

Se o maquinista quiser ganhar o máximo possível, quantas viagens precisará fazer?

1. 37
2. 51
3. 88
4. 89
5. 91

14. (Enem 2011) O número mensal de passagens de uma determinada empresa aérea aumentou no ano passado nas seguintes condições: em janeiro foram vendidas 33 000 passagens; em fevereiro, 34 500; em março, 36 000. Esse padrão de crescimento se mantém para os meses subsequentes. Quantas passagens foram vendidas por essa empresa em julho do ano passado?

1. 38 000
2. 40 500
3. 41 000
4. 42 000
5. 48 000

15. (Enem 2009) No gráfico seguinte está representado o aumento progressivo do número de horas de treino diário de um atleta ao longo dos 20 primeiros dias do mês de setembro, quando iniciou o treinamento.

Se for mantida essa tendência de crescimento, no último dia de setembro, o atleta deverá treinar, diariamente,

1. 7 horas e 30 minutos
2. 8 horas.
3. 9 horas.
4. 9 horas e 45 minutos.
5. 12 horas.