Análise Combinatória II

1. (Enem PPL 2019) Uma pessoa comprou um aparelho sem fio para transmitir músicas a partir do seu computador para o rádio de seu quarto. Esse aparelho possui quatro chaves seletoras e cada uma pode estar na posição 0 ou 1. Cada escolha das posições dessas chaves corresponde a uma frequência diferente de transmissão.

A quantidade de frequências diferentes que esse aparelho pode transmitir é determinada por

1. 6.
2. 8.
3. 12.
4. 16.
5. 24

Análise Combinatória

2. (Enem 2019) Durante suas férias, oito amigos, dos quais dois são canhotos, decidem realizar um torneio de vôlei de praia. Eles precisam formar quatro duplas para a realização do torneio. Nenhuma dupla pode ser formada por dois jogadores canhotos.

De quantas maneiras diferentes podem ser formadas essas quatro duplas?

1. 69
2. 70
3. 90
4. 104
5. 105

Análise Combinatória

3. (Enem 2019) Uma empresa confecciona e comercializa um brinquedo formado por uma locomotiva, pintada na cor preta, mais 12 vagões de iguais formato e tamanho, numerados de 1 a 12. Dos 12 vagões, 4 são pintados na cor vermelha, 3 na cor azul, 3 na cor verde e 2 na cor amarela. O trem é montado utilizando-se uma locomotiva e 12 vagões, ordenados crescentemente segundo suas numerações, conforme ilustrado na figura.

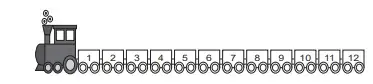
De acordo com as possíveis variações nas colorações dos vagões, a quantidade de trens que podem ser montados, expressa por meio de combinações, é dada por

1. $C_{12}^{4}x{C}_{12}^{3}x{C}_{12}^3{X}_{12}^2$
2. $C_{12}^{4}x{C}_8^{3}x{C}_5^3{X}_2^2$
5. $C_{12}^{4}x{C}_8^{3}x{C}_5^3{X}_2^2$

4. (Enem 2018) Torneios de tênis, em geral, são disputados em sistema de eliminatória simples. Nesse sistema, são disputadas partidas entre dois competidores, com a eliminação do perdedor e promoção do vencedor para a fase seguinte. Dessa forma, se na 1ª fase o torneio conta com 2n competidores, então na 2ª fase restarão n competidores, e assim sucessivamente até a partida final.

Em um torneio de tênis, disputado nesse sistema, participam 128 tenistas.

Para se definir o campeão desse torneio, o número de partidas necessárias é dado por:

1. 2 X 128
2. 64 + 32 + 16 + 8 + 4 + 2
3. 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1
4. 128 + 64 + 32 + 16 + 8 + 4 + 2
5. 64 + 32 + 16 + 8 + 4 + 2 + 1

5. (Enem 2018) O Salão do Automóvel de São Paulo é um evento no qual vários fabricantes expõem seus modelos mais recentes de veículos, mostrando, principalmente, suas inovações em design e tecnologia.

(Disponível em: http://g1.globo.com. Acesso em: 4 fev. 2015 - adaptado)

Uma montadora pretende participar desse evento com dois estandes, um na entrada e outro na região central do salão, expondo, em cada um deles, um carro compacto e uma caminhonete.

Para compor os estandes, foram disponibilizados pela montadora quatro carros compactos, de modelos distintos, e seis caminhonetes de diferentes cores para serem escolhidos aqueles que serão expostos. A posição dos carros dentro de cada estande é irrelevante.

Uma expressão que fornece a quantidade de maneiras diferentes que os estandes podem ser compostos é:

1. $A_{10}^4$
2. $C_{10}^4$
3. $C_4^{2}X{C}_6^2$ X 2 X 2
4. $A_4^{2}X{C}_6^2$ X 2 X 2
5. $C_4^{2}X{C}_6^2$

6. (Enem 2017) Um brinquedo infantil caminhão-cegonha é formado por uma carreta e dez carrinhos nela transportados, conforme a figura.

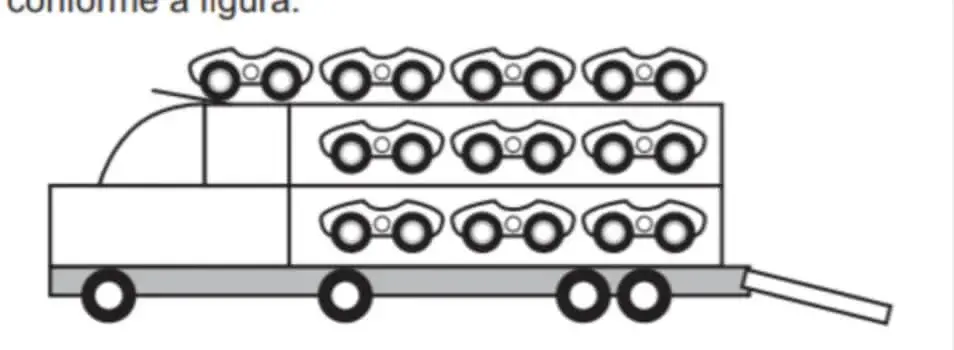
No setor de produção da empresa que fabrica esse brinquedo, é feita a pintura de todos os carrinhos para que o aspecto do brinquedo fique mais atraente. São utilizadas as cores amarelo, branco, laranja e verde, e cada carrinho é pintado apenas com uma cor. O caminhão-cegonha tem uma cor fixa. A empresa determinou que em todo caminhão-cegonha deve haver pelo menos um carrinho de cada uma das quatro cores disponíveis. Mudança de posição dos carrinhos no caminhão-cegonha não gera um novo modelo do brinquedo.

Com base nessas informações, quantos são os modelos distintos do brinquedo caminhão-cegonha que essa empresa poderá produzir?

1. C_6,4
2. C_9,3
3. C_10,4
4. 6⁴
5. 4⁶

7. (Enem 2017) Uma empresa especializada em conservação de piscinas utiliza um produto para tratamento da água cujas especificações técnicas sugerem que seja adicionado 1,5 mL desse produto para cada 1 000 L de água da piscina. Essa empresa foi contratada para cuidar de uma piscina de base retangular, de profundidade constante igual a 1,7 m, com largura e comprimento iguais a 3 m e 5 m, respectivamente. O nível da lâmina d’água dessa piscina é mantido a 50 cm da borda da piscina.

A quantidade desse produto, em mililitro, que deve ser adicionada a essa piscina de modo a atender às suas especificações técnicas é

1. 11,25.
2. 27,00.
3. 28,80.
4. 32,25.
5. 49,50.

8. (Enem 2017) A figura ilustra uma partida de Campo Minado, o jogo presente em praticamente todo computador pessoal. Quatro quadrados em um tabuleiro 16 x 16 foram abertos, e os números em suas faces indicam quantos dos seus 8 vizinhos contêm minas (a serem evitadas). O número 40 no canto inferior direito é o número total de minas no tabuleiro, cujas posições foram escolhidas ao acaso, de forma uniforme, antes de se abrir qualquer quadrado.

Em sua próxima jogada, o jogador deve escolher dentre os quadrados marcados com as letras P, Q, R, S e T um para abrir, sendo que deve escolher aquele com a menor probabilidade de conter uma mina.

O jogador deverá abrir o quadrado marcado com a letra

1. P.
2. Q.
3. R.
4. S.
5. T.

9. (Enem 2017) Uma bicicleta do tipo mountain bike tem uma coroa com 3 engrenagens e uma catraca com 6 engrenagens, que, combinadas entre si, determinam 18 marchas (número de engrenagens da coroa vezes o número de engrenagens da catraca).

Os números de dentes das engrenagens das coroas e das catracas dessa bicicleta estão listados no quadro.

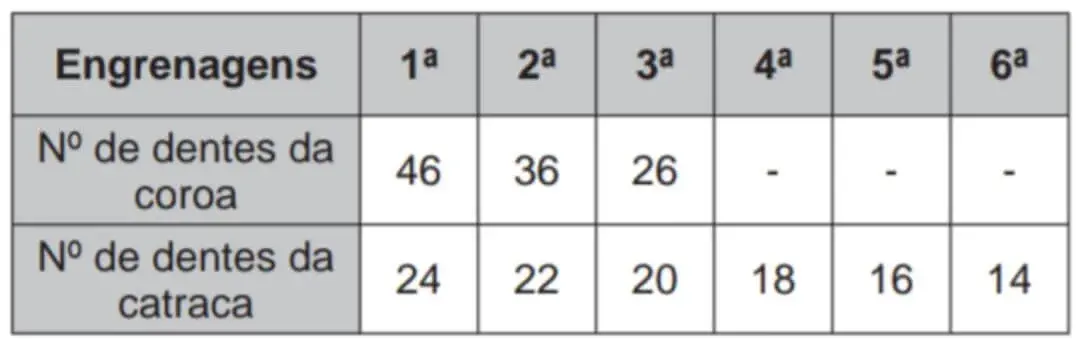
Sabe-se que o número de voltas efetuadas pela roda traseira a cada pedalada é calculado dividindo-se a quantidade de dentes da coroa pela quantidade de dentes da catraca.

Durante um passeio em uma bicicleta desse tipo, deseja-se fazer um percurso o mais devagar possível, escolhendo, para isso, uma das seguintes combinações de engrenagens (coroa x catraca):

A combinação escolhida para realizar esse passeio da forma desejada é

1. I
2. II
3. III
4. IV
5. V

10. (Enem 2017) O comitê organizador da Copa do Mundo 2014 criou a logomarca da Copa, composta de uma figura plana e o slogan “Juntos num só ritmo”, com mãos que se unem formando a taça Fifa. Considere que o comitê organizador resolvesse utilizar todas as cores da bandeira nacional (verde, amarelo, azul e branco) para colorir a logomarca, de forma que regiões vizinhas tenham cores diferentes.

De quantas maneiras diferentes o comitê organizador da Copa poderia pintar a logomarca com as cores citadas?

1. 15
2. 30
3. 108
4. 360
5. 972

11. (Enem 2017) Uma empresa construirá sua página na internet e espera atrair um público de aproximadamente um milhão de clientes. Para acessar essa página, será necessária uma senha com formato a ser definido pela empresa. Existem cinco opções de formato oferecidas pelo programador, descritas no quadro, em que “L” e “D” representam, respectivamente, letra maiúscula e dígito.

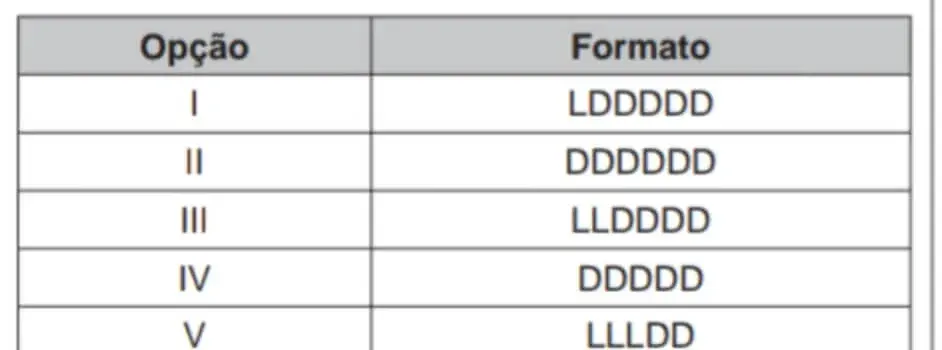
As letras do alfabeto, entre as 26 possíveis, bem como os dígitos, entre os 10 possíveis, podem se repetir em qualquer das opções.

A empresa quer escolher uma opção de formato cujo número de senhas distintas possíveis seja superior ao número esperado de clientes, mas que esse número não seja superior ao dobro do número esperado de clientes.

A opção que mais se adequa às condições da empresa é

1. I.
2. II.
3. III.
4. IV.
5. V.

12. (Enem 2016) O tênis é um esporte em que a estratégia de jogo a ser adotada depende, entre outros fatores, de o adversário ser canhoto ou destro.

Um clube tem um grupo de 10 tenistas, sendo que 4 são canhotos e 6 são destros. O técnico do clube deseja realizar uma partida de exibição entre dois desses jogadores, porém, não poderão ser ambos canhotos.

Qual o número de possibilidades de escolha dos tenistas para a partida de exibição?

1. $\frac{\mathrm{10!}}{\mathrm{2!\; x\; 8!}}$ - $\frac{\mathrm{4!}}{\mathrm{2!\; x\; 2!}}$
2. $\frac{\mathrm{10!}}{\mathrm{8!}}$ - $\frac{\mathrm{4!}}{\mathrm{2!}}$
3. $\frac{\mathrm{10!}}{\mathrm{2!\; x\; 8!}}-\; 2$
4. $\frac{\mathrm{6!}}{\mathrm{4!}}+\; 4\; x\; 4$
5. $\frac{\mathrm{6!}}{\mathrm{4!}}+\; 6\; x\; 4$

13. (Enem 2016) Para cadastrar-se em um site, uma pessoa precisa escolher uma senha composta por quatro caracteres, sendo dois algarismos e duas letras (maiúsculas ou minúsculas). As letras e os algarismos podem estar em qualquer posição. Essa pessoa sabe que o alfabeto é composto por vinte e seis letras e que uma letra maiúscula difere da minúscula em uma senha.

Disponível em: www.infowester.com. Acesso em: 14 dez. 2012.

O número total de senhas possíveis para o cadastramento nesse site é dado por

1. 10^{2 .} 26²
2. 10^{2 .} 52²
3. 10^{2 .} 52^{2 .} $\frac{\mathrm{4!}}{\mathrm{2!}}$
4. 10^{2 .} 26^{2 .} $\frac{\mathrm{4!}}{\mathrm{2!}\mathrm{.}\mathrm{2!}}$
5. 10^{2 .} 52^{2 .} $\frac{\mathrm{4!}}{\mathrm{2!}\mathrm{.}\mathrm{2!}}$

14. (Enem 2014) Um cliente de uma videolocadora tem o hábito de alugar dois filmes por vez. Quando os devolve, sempre pega outros dois filmes e assim secessivamente. Ele soube que a videolocadora recebeu alguns lançamentos, sendo 8 filmes de ação, 5 de comédia e 3 de drama e, por isso, estabeleceu uma estratégia para ver todos esses 16 lançamentos. Inicialmente alugará, em cada vez, um filme de ação e um de comédia. Quando se esgotarem as possibilidades de comédia, o cliente alugará um filme de ação e um de drama, até que todos os lançamentos sejam vistos e sem que nenhum filme seja repetido.

De quantas formas distintas a estratégia desse cliente poderá ser posta em prática?

1. 20 × 8! + (3!) ²
2. 8! × 5! × 3!
3. $\frac{8!\times \; <!--\; multiplication\; sign\; -->5!\times \; <!--\; multiplication\; sign\; -->3!}{2^8}$
4. $\frac{8!\times \; <!--\; multiplication\; sign\; -->5!\times \; <!--\; multiplication\; sign\; -->3!}{2^2}$
5. $\frac{16!}{2^8}$

15. (Enem 2013) Um artesão de joias tem à sua disposição pedras brasileiras de três cores: vermelhas, azuis e verdes.

Ele pretende produzir joias constituı́das por uma liga metálica, a partir de um molde no formato de um losango não quadrado com pedras nos seus vértices, de modo que dois vértices consecutivos tenham sempre pedras de cores diferentes.

A figura ilustra uma joia, produzida por esse artesão, cujos vértices A, B, C e D correspondem às posições ocupadas pelas pedras.

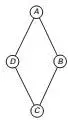
Com base nas informações fornecidas, quantas joias diferentes, nesse formato, o artesão poderá obter?

1. 6
2. 12
3. 18
4. 24
5. 36

16. (Enem 2012) O designer português Miguel Neiva criou um sistema de sı́mbolos que permite que pessoas daltônicas identifiquem cores. O sistema consiste na utilização de sı́mbolos que identificam as cores primárias (azul, amarelo e vermelho). Além disso, a justaposição de dois desses sı́mbolos permite identificar cores secundárias (como o verde, que é o amarelo combinado com o azul). O preto e o branco são identificados por pequenos quadrados: o que simboliza o preto é cheio, enquanto o que simboliza o branco é vazio. Os sı́mbolos que representam preto e branco também podem estar associados aos sı́mbolos que identificam cores, significando se estas são claras ou escuras.

Folha de São Paulo. Disponı́vel em: www1.folha.uol.com.br. Acesso em: 18 fev. 2012 (adaptado).

De acordo com o texto, quantas cores podem ser representadas pelo sistema proposto?

1. 14
2. 18
3. 20
4. 21
5. 23

17. (Enem 2012) O diretor de uma escola convidou os 280 alunos de terceiro ano a participarem de uma brincadeira. Suponha que existem 5 objetos e 6 personagens numa casa de 9 cômodos; um dos personagens esconde um dos objetos em um dos cômodos da casa. O objetivo da brincadeira é adivinhar qual objeto foi escondido por qual personagem e em qual cômodo da casa o objeto foi escondido.

Todos os alunos decidiram participar. A cada vez um aluno é sorteado e dá a sua resposta. As respostas devem ser sempre distintas das anteriores, e um mesmo aluno não pode ser sorteado mais de uma vez. Se a resposta do aluno estiver correta, ele é declarado vencedor e a brincadeira é encerrada.

O diretor sabe que algum aluno acertará a resposta porque há

1. 10 alunos a mais do que possı́veis respostas distintas.
2. 20 alunos a mais do que possı́veis respostas distintas.
3. 119 alunos a mais do que possı́veis respostas distintas.
4. 260 alunos a mais do que possı́veis respostas distintas.
5. 270 alunos a mais do que possı́veis respostas distintas.

18. (Enem 2011) O setor de recursos humanos de uma empresa vai realizar uma entrevista com 120 candidatos a uma vaga de contador. Por sorteio, eles pretendem atribuir a cada candidato um número, colocar a lista de números em ordem numérica crescente e usá-la para convocar os interessados. Acontece que, por um defeito do computador, foram gerados números com 5 algarismos distintos e, em nenhum deles, apareceram dı́gitos pares. Em razão disso, a ordem de chamada do candidato que tiver recebido o número 75 913 é

1. 24.
2. 31.
3. 32.
4. 88.
5. 89.

19. (Enem 2011) Um técnico em refrigeração precisa revisar todos os pontos de saı́da de ar de um escritório com várias salas.

Na imagem apresentada, cada ponto indicado por uma letra é a saı́da do ar, e os segmentos são as tubulações.

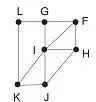
Iniciando a revisão pelo ponto K e terminando em F, sem passar mais de uma vez por cada ponto, o caminho será passando pelos pontos

1. K, I e F.
2. K, J, I, G, L e F.
3. K, L, G, I, J, H e F.
4. K, J, H, I, G, L e F.
5. K, L, G, I, H, J e F.

20. (Enem 2010) João mora na cidade A e precisa visitar cinco clientes, localizados em cidades diferentes da sua. Cada trajeto possı́vel pode ser representado por uma sequência de 7 letras. Por exemplo, o trajeto ABCDEFA, informa que ele sairá da cidade A, visitando as cidades B, C, D, E e F nesta ordem, voltando para a cidade A. Além disso, o número indicado entre as letras informa o custo do de deslocamento entre cada uma das cidades.

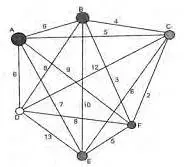
Como João quer economizar, ele precisa determinar qual o trajeto de menor custo para visitar os cinco clientes. Examinando a figura, percebe que precisa considerar somente parte das sequências, pois os trajetos ABCDEFA e AFEDCBA têm o mesmo custo. Ele gasta 1min 30s para examinar uma sequência e descartar sua simétrica, conforme apresentado. O tempo mı́nimo necessário para João verificar todas as sequências possı́veis no problema é de

1. 60 min.
2. 90 min.
3. 120 min.
4. 180 min.
5. 360 min

21. (Enem 2009) Doze times se inscreveram em um torneio de futebol amador. O jogo de abertura do torneio foi escolhido da seguinte forma: primeiro foram sorteados 4 times para compor o Grupo A. Em seguida, entre os times do Grupo A, foram sorteados 2 times para realizar o jogo de abertura do torneio, sendo que o primeiro deles jogaria em seu próprio campo, e o segundo seria o time visitante.

A quantidade total de escolhas possı́veis para o Grupo A e a quantidade total de escolhas dos times do jogo de abertura podem ser calculadas através de

1. uma combinação e um arranjo, respectivamente.
2. um arranjo e uma combinação, respectivamente.
3. um arranjo e uma permutação, respectivamente.
4. duas combinações.
5. dois arranjos.

22. (Enem 2009) Para cada indivı́duo, a sua inscrição no Cadastro de Pessoas Fı́sicas (CPF) é composto por um número de 9 algarismos e outro número de 2 algarismos, na forma d₁ d₂, em que os dı́gitos d₁ e d₂ são denominados dı́gitos verificadores. Os dı́gitos verificadores são calculados, a partir da esquerda, da seguinte maneira: os 9 primeiros algarismos são multiplicados pela sequência 10, 9, 8, 7, 6, 5, 4, 3, 2 (o primeiro por 10, o segundo por 9, e assim sucessivamente); em seguida, calcula-se o resto r da divisão da soma dos resultados das multiplicações por 11, e se esse resto r for 0 ou 1, d¹ é zero, caso contrário d¹ = (11 − r). O dı́gito d 2 é calculado pela mesma regra, na qual os números a serem multiplicados pela sequência dada são contados a partir do segundo algarismo, sendo d¹ o último algarismo, isto é, d² é zero se o resto s da divisão por 11 das somas das multiplicações for 0 ou 1, caso contrário, d² = (11 − s). Suponha que João tenha perdido seus documentos, inclusive o cartão de CPF e, ao dar queixa da perda na delegacia, não conseguisse lembrar quais eram os dı́gitos verificadores, recordando-se apenas que os nove primeiros algarismos eram 123.456.789. Neste caso, os dı́gitos verificadores d¹ e d² esquecidos são, respectivamente,

1. 0 e 9.
2. 1 e 4.
3. 1 e 7.
4. 9 e 1.
5. 0 e 1.