Razão e Escala

A noção de relação algébrica em matemática é importante para representar de modo geral as relações que estabelecemos entre duas grandezas – razão entre ‘a’ e ‘b’, expressa por a/b. De modo geral aplicamos nas relações algébricas entre duas proporções a regra de proporcionalidade: “O produto dos meios é igual ao produto dos extremos”.

Esta regra é bastante útil em matemática (proporcionalidade direta) é frequentemente conhecida como “regra de três”. Sua utilidade vai desde o cálculo de porcentagens até a resolução de problemas com proporção direta e inversa (grandezas direta ou inversamente proporcionais). Primeiramente vamos nos ater a noção de razão e proporção em Matemática.

Razões

Existem várias maneiras de comparar duas grandezas. Por exemplo, quando se escreve a > b (lê-se “a” maior do que “b”) ou a < b ou ainda (lê-se “a” menor do que “b”) e a = b (lê-se “a” igual ao “b”), estamos comparando as grandezas a e b. Essa comparação pode ser feita através de uma razão entre as duas grandezas, isto é, o quociente entre essas grandezas. Em resumo, uma razão é a representação da divisão entre dois valores “a” e “b”.

Exemplo:

A razão entre 6 e 3 é expressa por 6:3 ou 6/3. Se pretendemos comparar a e b determino a razão a : b ou a/b, Mas se dissermos que a razão entre elas é 2, estamos afirmando que “a” é duas vezes maior que “b”, ou seja, o dobro.

Aplicações

Entre as aplicações práticas de razões especiais, as mais comuns, são:

1. Velocidade média

A velocidade média em geral é uma grandeza obtida pela razão entre uma distância percorrida e um tempo gasto neste percurso.

Exemplo 1:

1. Suponhamos que um carro percorreu 120km em 2 horas. A velocidade média do carro nesse percurso será calculada a partir da razão:

O que significa que, em 1 hora o carro percorreu 60km.

2. Escala

Escala é a comparação (através da razão) entre o comprimento observado no desenho (mapa, por exemplo) e o comprimento real correspondente, ambos na mesma unidade de medida.

Exemplo 2:

Em um mapa, um comprimento de 8m está representado por 16cm. Qual a escala usada para fazer esse mapa?

8m = 800cm.

Escala = 16cm/800cm = 1/50 ou ainda escala 1:50, como é mais comum nos desenhos e mapas.

Isto significa que cada 1cm medido no desenho é igual 50cm no tamanho no real.

3. Densidade Demográfica

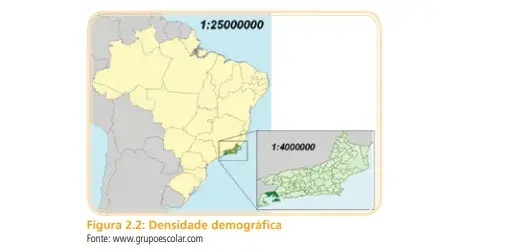
O cálculo da densidade demográfica chamada de população relativa de uma região, também é considerado uma aplicação de razão entre duas grandezas.

Ela expressa a relação entre o número de habitantes e a área em uma região.

Exemplo 3:

Um município ocupa a área de 100.000km². E, de acordo com o censo realizado, tem população aproximada de 5.000 habitantes. A densidade demográfica desse município é obtida assim:

Isto significa que para cada 1 quilômetro quadrado, esse município tem 20 habitantes.

Para o nosso caso mais específico de finanças, um exemplo de razão é relacionar a noção de razão com a transformação de frações em números decimais (com vírgula). Vejamos alguns exemplos:

A razão 20:2, ou 20/10 é igual à 10. A razão de 20 para 2 é 10, ou seja vinte é dez vezes maior do que dois.

A razão 12:3 ou 12/3 é igual a quatro, ou seja doze é quatro vezes maior que três.

A razão 4/6: 4/6 é igual a 1. A razão de 4/6 para 4/6 é 1 (um inteiro ou 100%).

A razão facilita o entendimento de alguns problemas, até mesmo financeiros, do dia a dia. É o que veremos a seguir.

Exemplo prático:

A informação de que um produto que queremos comprar aumentou em R$25,00, como sabermos se foi um aumento significativo? Como descobrir se vale à pena comprar naquele momento ou esperar por uma promoção?

De modo analítico, podemos comparar o valor do aumento com o valor do produto, para analisar a razão do aumento, isto é, o quanto aumentou em relação ao valor inicial.

Se o produto valia R$1.000,00, devemos achar a razão de 25 para 1.000. Esta razão é igual a 0,025, ou 5%. Sabemos que o produto aumentou em 2,5%. Porém se o produto valia R$100,00 teremos a razão de 25 para 100, isto é, o produto aumentou em 25%.

Com este modo de analisar os valores podemos tomar a decisão, financeira, de comprar ou não o produto. Vale ressaltar que, neste caso, não estamos levando em consideração outros fatores que ajudariam na decisão, como os juros, riscos e o chamado custo de oportunidade do capital. Estes fatores serão considerados mais adiante na disciplina.

As situações apresentadas destacam a linguagem mais utilizada nas finanças como um todo: a porcentagem.