Proporção e Regra de três
Na aula de hoje, revisaremos proporcionalidade (regra de três). Nosso objetivo é propiciar maior entendimento e exploração de conceitos matemáticos fundamentais à dedução de relações algébricas (fórmulas) úteis aos cálculos de Matemática na obtenção de leis gerais.

Sempre que utilizarmos a regra de três no intuito de determinar porcentagens, devemos relacionar a parte do todo com o valor de 100%. Alguns exemplos demonstrarão como devemos proceder com a regra de três envolvendo cálculos percentuais.
Obs.: Nas situações envolvendo porcentagens realizamos a propriedade “produtos dos meios é igual ao produto dos extremos”, por ser grandeza diretamente proporcional.
Exemplo:

Regra de três direta ou Regra de Três Simples
“Regra de três simples” é um processo prático para resolver problemas que envolvem quatro valores dos quais conhecemos três deles. Devemos, portanto, determinar um valor a partir dos três já conhecidos.
Passos didáticos utilizados para resolver problemas com a regra de três simples
1º Passo: Construir uma tabela, agrupando as grandezas da mesma espécie em colunas e mantendo na mesma linha as grandezas de espécies diferentes em correspondência.
2º Passo: Identificar se as grandezas são direta ou inversamente proporcionais.
3º Passo: Montar a proporção e resolver a equação.
Questão 1:
Em uma sala de 40 alunos realizou-se uma pesquisa, a qual apontou que 30 alunos gostam de pescaria. Qual é a porcentagem de alunos que gostam de pescaria?


Regra de três inversa
Ao resolver problemas que envolvam grandezas (entendemos por grandeza tudo aquilo que pode ser medido, contado) devemos tomar alguns cuidados em relação à proporcionalidade ser direta ou inversa.
Por exemplo, em uma corrida quanto maior for a velocidade, menor será o tempo gasto nessa prova. Aqui as grandezas são a velocidade e o tempo e trata-se de grandezas inversamente proporcionais.
Importante
Duas grandezas são inversamente proporcionais quando, dobrando uma delas, a outra se reduz para a metade; triplicando uma delas, a outra se reduz para a terça parte. E assim por diante.
Questão 2:
Um trem, deslocando-se a uma velocidade média de 400km/h, faz um determinado percurso em 3 horas. Em quanto tempo faria esse mesmo percurso, se a velocidade utilizada fosse de 480km/h?

Solução: montando a tabela:
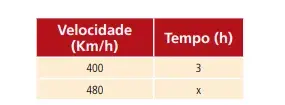
Identificação do tipo de relação:
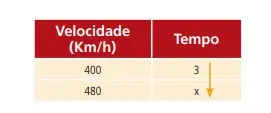
Inicialmente colocamos uma seta para baixo na coluna que contém o x (2ª coluna).
Observe que Aumentando a velocidade, o tempo do percurso diminui.
Como as palavras são contrárias (aumentando - diminui), podemos afirmar que as grandezas são inversamente proporcionais. Assim sendo, colocamos outra seta no sentido contrário (para cima) na 1ª coluna. Montando a proporção e resolvendo a equação temos:

Logo, o tempo desse percurso seria de 2,5 horas ou 2 horas e 30 minutos.
Maior velocidade menor tempo de percurso, ou seja, grandezas inversamente proporcionais.

Assim: O tempo gasto é de 1,67 horas.
Para saber quantos minutos e segundos precisamos de mais uma “regra de três”:

1/5 . 60 = 60/5 = 12 segundos
Assim: O tempo gasto em horas, minutos e segundos é: 1 hora, 40 minutos e 12 segundos.
Proporção e Escala

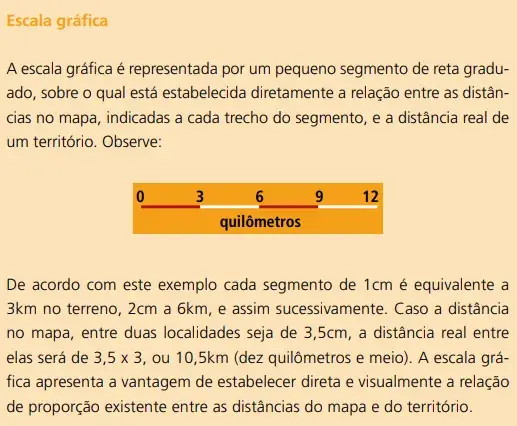



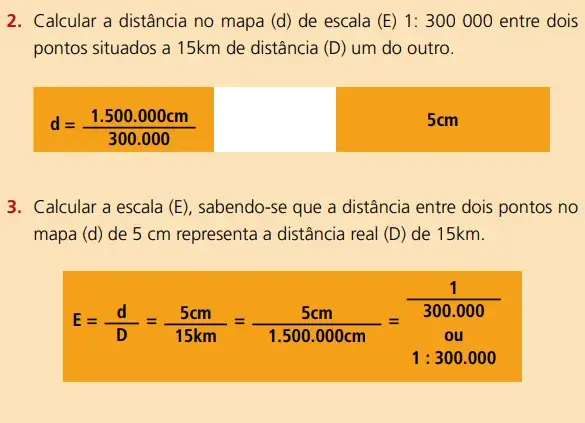
Referências:
JUNIOR, Roberto José Medeiros. Matemática II . Curitiba-PR: - e-Tec Brasil, 2011.