Vetores
Grandeza Escalar e Vetorial
G. Escalar: é aquela que fica perfeitamente definida quando conhecemos o seu valor numérico e a sua unidade de medida.
Ex.: massa, tempo, comprimento, energia, etc.
G. Vetorial: é aquela que fica perfeitamente definida, quando conhecemos além do valor numérico e da unidade de medida a direção e o sentido.
Ex: velocidade, aceleração, força, etc.
Vetor
Um vetor é um ente matemático representado por um segmento de reta orientado. Um vetor se caracteriza por ter módulo, direção e sentido.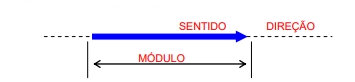
1. Vetores Iguais
Duas grandezas vetoriais são iguais quando apresentam o mesmo módulo, a mesma direção e o mesmo sentido.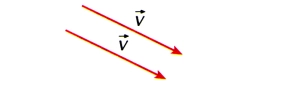
2. Vetores Opostos
Duas grandezas vetoriais são opostas quando apresentam o mesmo módulo, a mesma direção, mas sentidos contrários.
3. Adição de Vetores
a) Método do Polígono
b) Método do Paralelogramo
C) Módulo:
R² = R² = a² = b² + 2.a.b.cosα
1°) Com mesma direção e mesmo sentido (α = 0°)
2°) Com mesma direção e sentidos opostos (α = 180°):
3°) Ortogonais (α = 90°):
4. Diferença De Dois Vetores
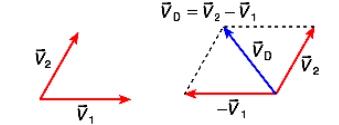
ou
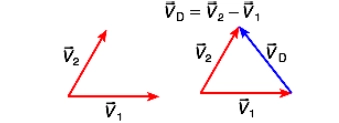
VD² = V1² + V2² -2.V1.V2 .cosθ;
5. Produto De Um Escalar Por Um Vetor
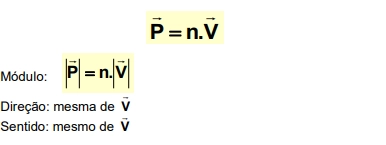
Ex:
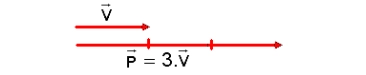
Se o vetor V⟶ tem módulo V = 2 unidades, logo o vetor resultante tem módulo P = 6 unidades (P= 3.2 = 6 unidades)
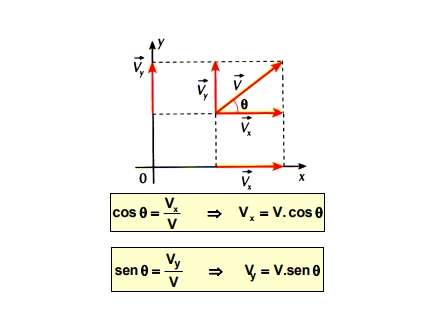
6. Componentes De Um Vetor
